Type Annotations
In TypeScript,type annotations offer a way to define (or annotate) the data types of variables, class members, function parameters and return values.
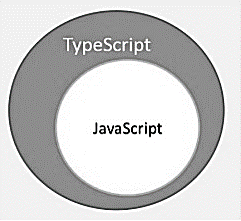
TypeScript is a statically typed programming language that optionally supports the dynamic typing. Because of this support any JavaScript file (.js) can be directly renamed as a TypeScript file (.ts). As we know JavaScript is a dynamically typed programming language and TypeScript is the superset of the JavaScript. TypeScript supports all the functionalities of JavaScript plus some additional features.
TypeScript provides the way how to annotate the datatype. By the term “type annotations” means assigning the datatypes.
Variable Type Annotations
TypeScript supports static typing of variables. We can annotate the types of variables while declaring them. Also TypeScript optionally support the dynamic typing as JavaScript.
For example, when we define a variable that holds a number, we can define it as follows –
var x =10;The above declaration is absolutely permissible in TypeScript as it supports the dynamic typing.
We can annotate the datatype of the variable x as follows
var x:number=10;To do a type annotation, you can use colon (:) sign after the variable name followed by datatype of the variable.
var varName: datatype
Followings are the different examples to annotate a variable with different datatypes.
let name:string;let age:number;let isEnrolled:boolean;In the example above, we added string as type of variable name. Similarly, age and isEnrolled are annotated with number and boolean type.
Example
Let’s try the following example. In this example, we have declared two variables, pName, and pAge. We have annotated pName as string and pAge as number.
let pName:string;let pAge:number;
pName ="John Doe";
pAge =35;console.log(Name of the person is ${pName} and his age is ${pAge});On compiling, TypeScript compiler will produce the following JavaScript code
let pName;let pAge;
pName ="John Doe";
pAge =35;
console.log(Name of the person is ${pName} and his age is ${pAge});The output of the above JavaScript code is as follows
Name of the person is John Doe and his age is 35
Function Type Annotations
You can add the type to a function in TypeScript. A function’s type has two parts the function parameters and the return type of the function.
Function Parameter Type Annotation
We can annotate the datatypes of the parameters in the function definition.
functiondisplayDetails(id:number, name:string){console.log("ID:", id);console.log("Name", name);}displayDetails(123,"John");On compiling, it will produce the following JavaScript code
functiondisplayDetails(id, name){
console.log("ID:", id);
console.log("Name:", name);}displayDetails(123,"John");</code></pre>
The result of the above example code is as follows
ID: 123
Name: John
Function Return Type Annotation
You can add the datatype of the function return. It will be the datatype of the value returned by the function.
functionadd(x:number, y:number):number{return x + y;}
If you are not writing a return type then, the default return type of any function will be undefined.
If a function is not returning any value then, you should use void as function return type instead of leaving it off.
For example, instead of writing the following
functiongreet(name:string){console.log(Hello Mr. ${name}. Welcome to Tutorials Point.);}
Write the function using void as return type as follows
functiongreet(name:string):void{console.log(Hello Mr. ${name}. Welcome to Tutorials Point.);}
Example
In the example below, we annotate the function parameters and its return type. The function add take two parameters - x and, y of number type and also a value of number type. The returned value is the sum of the passed arguments to the function.
functionadd(x:number, y:number):number{return x + y;}console.log(add(2,3))
On compiling, it will produce the following JavaScript code
functionadd(x, y){return x + y;}
console.log(add(2,3));
The output of the above code is as follows −
5
Object Properties Type Annotations
You can use the type annotation to add the types to the properties of an object.
Let's define an object using interface as follows −
interfacePerson{
name:string;
age:number;}const person: Person ={
name:"John Doe",
age:35,}
In the above example, we added types string and number to the properties name and age respectively.
You can assign only string value to the name property and similarly only number value to the age property. Suppose if you try to add a string to age, it will throw an error.
Type 'string' is not assignable to type 'number'.
Example
Let's take a complete example. In this example, we define an interface named Person with two properties name and age. The name property is annotated as string and age is as number. We create an object named person using the interface Person. Then finally, we display the object properties in the console.
interfacePerson{
name:string;
age:number;}const person: Person ={
name:"John Doe",
age:35,}console.log(The person's name is ${person.name} and person's age is ${person.age});
On compiling, it will produce the following JavaScript code −
const person ={
name:"John Doe",
age:35,};
console.log(The person's name is ${person.name} and person's age is ${person.age});
The output of the above example code if as follows −
The person's name is John Doe and person's age is 35
The type annotations of variables, function parameters and return types, etc. are recommended in TypeScript. But also TypeScript supports dynamic typing as in JavaScript. As you already know that TypeScript supports all ECMAScript features.





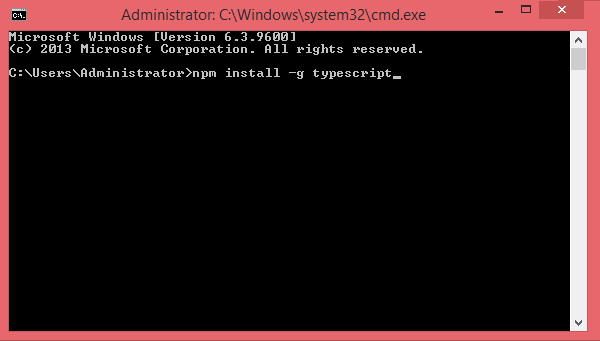
 to launch the setup process. This will only take a minute.
to launch the setup process. This will only take a minute.
 on the right-hand side of the editor. Enter typescript in the search box.
on the right-hand side of the editor. Enter typescript in the search box.
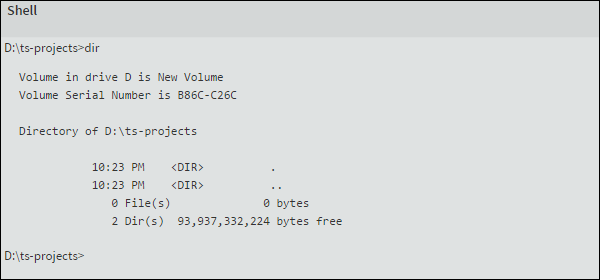
 . Once you click on the icon, you will see the shell window as shown below −
. Once you click on the icon, you will see the shell window as shown below −