You may encounter situations, when a block of code needs to be executed several number of times. In general, statements are executed sequentially: The first statement in a function is executed first, followed by the second, and so on.
Programming languages provide various control structures that allow for more complicated execution paths.
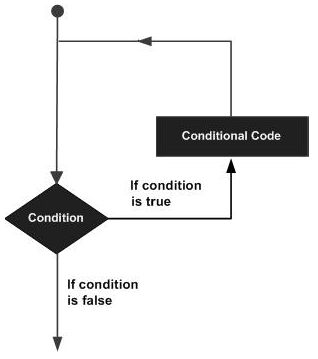
A loop statement allows us to execute a statement or group of statements multiple times. Given below is the general form of a loop statement in most of the programming languages.
TypeScript provides different types of loops to handle looping requirements. The following figure illustrates the classification of loops −
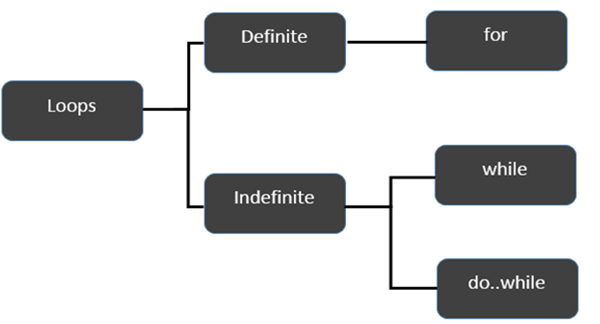
Definite Loop
A loop whose number of iterations are definite/fixed is termed as a definite loop. The for loop is an implementation of a definite loop.
| S.No. | Loops & Description |
|---|---|
| 1. | for loopThe for loop is an implementation of a definite loop. |
Indefinite Loop
An indefinite loop is used when the number of iterations in a loop is indeterminate or unknown.
Indefinite loops can be implemented using −
| S.No | Loops & Description |
|---|---|
| 1. | while loopThe while loop executes the instructions each time the condition specified evaluates to true. |
| 2. | do whileThe dowhile loop is similar to the while loop except that the do…while loop doesnt evaluate the condition for the first time the loop executes. |
Example: while versus do..while
var n:number=5while(n >5){console.log("Entered while")}do{console.log("Entered dowhile")}while(n>5)The example initially declares a while loop. The loop is entered only if the expression passed to while evaluates to true. In this example, the value of n is not greater than zero, hence the expression returns false and the loop is skipped.
On the other hand, the dowhile loop executes statement once. This is because the initial iteration does not consider the Boolean expression. However, for the subsequent iteration, the while checks the condition and takes the control out of the loop.
On compiling, it will generate following JavaScript code −
var n =5;while(n >5){console.log("Entered while");}do{console.log("Entered dowhile");}while(n >5);The above code will produce the following output −
Entered dowhile
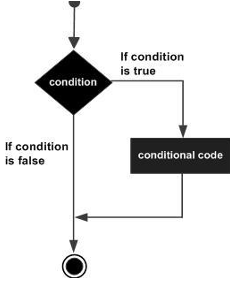
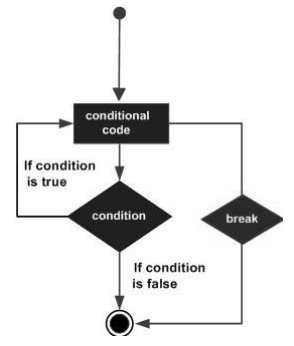
The break Statement
The break statement is used to take the control out of a construct. Using break in a loop causes the program to exit the loop. Its syntax is as follows −
Syntax
break
Flow diagram
Example
Now, take a look at the following example code −
var i:number=1while(i<=10){if(i %5==0){console.log("The first multiple of 5 between 1 and 10 is : "+i)break//exit the loop if the first multiple is found }
i++}//outputs 5 and exits the loopOn compiling, it will generate the following JavaScript code −
var i =1;while(i <=10){if(i %5==0){console.log("The first multiple of 5 between 1 and 10 is : "+ i);break;//exit the loop if the first multiple is found}
i++;}//outputs 5 and exits the loopIt will produce the following output −
The first multiple of 5 between 1 and 10 is : 5
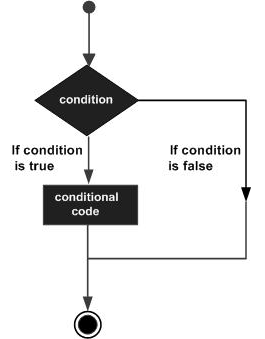
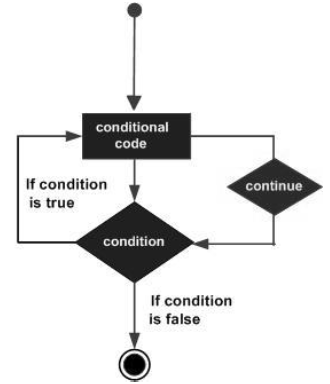
The continue Statement
The continue statement skips the subsequent statements in the current iteration and takes the control back to the beginning of the loop. Unlike the break statement, the continue doesnt exit the loop. It terminates the current iteration and starts the subsequent iteration.
Syntax
continue
Flowchart
Example
An example of the continue statement is given below −
var num:number=0var count:number=0;for(num=0;num<=20;num++){if(num %2==0){continue}
count++}console.log(" The count of odd values between 0 and 20 is: "+count)//outputs 10 The above example displays the number of odd values between 0 and 20. The loop exits the current iteration if the number is even. This is achieved using the continue statement.
On compiling, it will generate following JavaScript code.
var num =0;var count =0;for(num =0; num <=20; num++){if(num %2==0){continue;}
count++;}console.log(" The count of odd values between 0 and 20 is: "+ count);//outputs 10Output
The count of odd values between 0 and 20 is: 10
The Infinite Loop
An infinite loop is a loop that runs endlessly. The for loop and the while loop can be used to make an endless loop.
Syntax: Infinite Loop using for loop
for(;;) {
//statements
}
Example: Infinite loop using for loop
for(;;){console.log(This is an endless loop)}Syntax: Infinite loop using while loop
while(true) {
//statements
}
Example: Infinite loop using while loop
while(true){console.log(This is an endless loop)}