Author: saqibkhan

Artificial Intelligence (AI) Frames are data models that depict stereotypical conditions or notions to enable systems to encode and manipulate knowledge, be it effectively or efficiently. Frames Marvin Minsky introduced frames in the 1970s, which decompose information into slots (attributes) and values, similar to objects in object-oriented programming. These are important in information representation and reasoning so that, given incomplete information, the machine can infer, generalize and work with information.

Frames have a lot of applications in such fields as natural language processing, expert systems and vision. Knowledge structuring in making an AI system emulate human-like processes, frames are important because they help to conceptually model a contextual knowledge structure, which would be a fundamental concept of symbolic AI and cognitive modeling.

Structure of a Frame

Struts and Plugs

Frames consist of slots, which are analogous to attributes or properties, and of fillers, or the values given them. All the slots determine some part of the specific knowledge applying to the given concept of the frame. An instance of this point is that a frame called a car may have slots called Color, Brand, and Type, the fillers being Red, Toyota and Petrol. These fillers may either be fixed values or dynamic processes, as well as references to other frames.

This framework enables robots to have extensive ordered knowledge in the same way human beings obtain it. The flexibility and adaptability to complicated knowledge bases of the frame model come with its division or structure (slots) and content (fillers).

Defaults and Inheritance

Default values Slots in a frame may include default values when given no value. This is an efficient property since it creates a possibility to generalize and specialize. Usage example: the default type of fuel for a generic frame of a vehicle type can be set to the type Petrol, which can be changed by a specialization frame of an Electric Car (the specific type of fuel can be Electricity).

The inheritance is supported in this hierarchical structure, where the sub-frames inherit properties of the frame they are part of unless modified. This reflects the patterns of object-oriented programming in software development and better facilitate reasoning since a system may infer some missing aspects by using default or inherited slots.

Procedural Attachments

Frames do not only represent some pre-procedural strips but may equally include procedural attachments. These are tiny executable functions or routines which are attached to slots. Typical ones are:

• If-Needed: Supplied when a slot has a value that is needed but missing.
• If-Added: Investigated the case when another value is assigned to a slot.
• If-Removed: It is executed when the value of a slot is removed.

These attachments enable activity and smart reaction in the course of reasoning, which allows the system to carry out functions such as calculation of value, slot verification or looking up data. This interaction transforms frames beyond storing and makes frames contribute to the decision-making of AI systems.

Nested Frames, Linked Frames

Other frames may be slots filled by other frames, which are called nested frames. This permits hierarchically complex knowledge representation. To take an example, a frame representing a Person might include a slot named Address whose filler is an Address frame with slots such as Street, City and Zip Code. During such a compositionality, frames can characterize real-life relationships and objects in a very structured form.

Frames may further be coupled to each other, thus creating a network or a graph-like interconnection of knowledge structures. Such associations aid the formation of semantic networks, which improve inference and contextualization.

Frames of the Instance and Class

Frames are normally categorized into the following two types: instance frame and class frame. A class frame defines typical properties of a number of individuals (e.g., ‘Dog is the class’), whereas an instance frame defines some specific object (e.g., ‘Fido is an individual dog’). Instance frames automatically inherit the property of a class frame and this streamlines knowledge organization.

The class frames are template-like and instance frames are those that bring values depending on the template. Such a separation favors abstraction and particularity in logical thinking. It is particularly handy in areas such as object recognition or medical diagnostics, in which classes establish symptoms and instances establish particular patient data.

Types of Frames

Class Frames

Class frames are the form of categories or concepts which have general characteristics. They act as blueprints, which determine the structure and abnormal values of a selection of similar objects. As a case in point, a class frame, that is, to say, a frame of the word Bird, may comprise slots such as Has Wings = Yes, Can Fly = (Usually), as well as Number of Legs = 2.

More specific subclasses or instance frames may inherit these slots. Class frames are also important in the systematic development of the hierarchic representation of knowledge since they result in excellent reuse, minimal redundancy, and the ability to reason through inheritance. Class frames in many AI systems are the basis of the abstract and generalized modelling of real-world domains.

Instance Frames

There are instance frames that reflect particular objects or entities based on the class frames. They will have inherited structure and default values of the parent class frames and can override some values as well. In some cases (such as the example of the class frame Bird with a slot Can Fly set to = Usually), an instance frame of Penguin may override it to set Can Fly to = No.

This arrangement enables AI systems to separate general information and certain facts. The expert systems make extensive use of instance frames, in which there are case-based data to handle, as well as generic rules, due to the synthesis of the inherited knowledge with definite slot values.

Static Frames

Those that are fixed in nature are called static frames because the values in the slots never change during the functioning of the system. Frames are concepts or things that have fixed properties, e.g., mat, mathematical objects or physical constants. To take an example, a frame named “Pi” could contain a non-changing slot as (Value = 3.14159). The domain of use of static frames is normally in areas where the knowledge is fixed and understands the same thing.

In rule and deterministic systems, these are significant, as predictability and the certainty of knowledge are crucial. They are very convenient when encoding a factual nature, which is not interchangeable by context or time, like settings of systems or fundamental constants in science.

Dynamic Frames

Dynamic frame differs from the static frame as their slot values can vary during run time. Such frames are applicable in systems where a response to changing data or interactive input is required, like real-time systems and conversational agents. In other words, a frame that acts as a chat user may deal with the change of the “Current Mood” field according to new information.

Procedural attachments (i.e., a procedural attachment such as an if-needed or an if-added) are often included in dynamic frames to cause actions or calculations to occur when slot values are changed. This implies that they can be applied in adaptive learning, robotics, and user modelling since we need incessant updates in the knowledge base to make the right decisions.

Frames about Frames

Other frames can be described or regulated through meta-frames. They offer information of a higher level, e.g., rules of inheritance, constraints or logic of reasoning used against other frames. They find application in both dynamic rule creation and debugging in knowledge-based systems. It also bears metadata relating to relationships between other frames, which can be stored in meta-frames to increase flexibility and control.

They are especially useful in more complicated reasoning systems where the logic over which the behaviour of the frame components should be executed must be somehow explicitly represented and updated throughout execution.

Frame-Based Knowledge Representation

Comprehension of Frame

Knowledge representation of a frame is a form of knowledge representation that is used in AI to organize and store knowledge using frames, which are data structures. Information in each frame is represented in the form of slots (attributes) and fillers (values) of an object or situation. This representation reflects an anthropomorphic way humans attach properties and behaviour to things. As an example, a Dog frame could contain slot fields of Breed, Color and Barks=Yes.

Frames offer contextual, modular, and structured formats, which are more simplified to be interpreted and operated by AI systems. It has the advantage of supporting inheritance, procedural knowledge and default reasoning and is therefore very applicable in areas where conceptual relationships are critical, e.g. medical diagnosis or natural language processing.

Hierarchy Organization and Inheritance

Among the advantages of frame-based systems is hierarchical structure. It is possible to structure frames in a taxonomy, with general frames (class frames) at the top and specific (instance frames) containing inherited properties. As an example, a frame-called Vehicle may be a parent of a Car and Bike, which in turn have their children. The inheritance results in a lessening of redundancy as common attributes can be declared once and then reused.

Furthermore, it provides the capability of making the AI systems reason incomplete data through default slot values and overrode mechanisms. Inheritance can also be used to manage memory, perform abstractions and recognition of patterns in knowledge-intensive applications.

Procedural and Contextual Knowledge Management

Frames are not just simple holders of data; they can have a procedural attachment to execute some actions or to access slot values dynamically. Examples: These can be triggers such as IF-NEEDED, IF-ADDED or IF-REMOVED, which are executed when a slot is read/written/cleared. An example would be that when a robot has access to the cell of Battery-Level, an IF-NEEDED procedure would be initiated to verify the current status of the battery and update it.

This lets the system describe not only facts but also actions or calculations on them. It has found particular applications in expert systems, INTERACTIVE interfaces and adaptive learning systems in which dynamics of reasoning and interactivity are essential.

Comparisons to Other Representations

Frame-based systems provide a more natural and ordered form of representation compared with logic-based such as predicate logic or semantic networks. Predicate logic is also an option, but it is more often less practical when trying to represent complex relationships or default values, being mathematically rigorous. Semantic networks are graphical. However, these structures do not have the input-output slot-filler results like frames, as well as specific procedural mechanisms.

Frames, conversely, offer the template-based, object-oriented paradigm that is very close to human psychic functions. This renders them simpler to apply in fields such as user modelling, natural language processing and visual recognition. Besides, the flexibility and scaling of the frames is made possible by the modularity.

Inference in Frame Systems

Slot-Based Reasoning

Within the frame systems, it is easy to see how reasoning may commence with slot-based inference, with the system extracting inferences based on the values of a slot in a frame. Upon query, the AI system verifies whether the necessary information is there in the slot or not. Otherwise, it might trigger procedural attachments (such as if needed) to calculate or fetch the value dynamically. This process enables effective and situational inference particularly in expert systems.

As an example, a procedure can assign a value to the slot of a “Risk Level” in a “Patient” frame in case it is not filled with any value based on the symptoms and age. Slot-based informatics allows context on-the-fly responses without resorting to full-blown rules engines.

Overriding and Inheritance Mechanism

One of the important attributes of frame-based inference is inheritance in that sub-frames automatically inherit slot values of parent (class) frames. This aids in the reuse of knowledge and reasoning where information is not complete. An instance frame of a type, e.g., a “Dog” instance frame, inherits family, i.e., inherits Has Legs = 4, of another kind, e.g., a “Mammal” class frame, unless it overrides it. This allows AI systems to infer the missing information by going up the hierarchy until a default or inherited value can be located.

In contrast, the overriding feature enables the replacement of inherited values in more specific frames- affecting specialization. These mechanisms, as a whole, allow reasoning to be made naturally in well-founded hierarchies, quite similar to the way humans reason logically.

Default Reasoning

Frame systems enable default reasoning, in which slots can be pre-defined with values assumed whenever no other value is specified. It is handy in the case of general-knowledge-based assumptions. When the slot under the keyword “Fuel Type” of a frame called a “Vehicle” is blank, the system can assume that the value is defaulted to “Petrol.” This allows a continuity in thinking without the necessity to enter all the data manually.

Default values fulfil the role of safe fallbacks based on generally accepted facts. Default inference enables the AI to make an educated guess, making it more responsive and less reliant on user feedback or entire sets of data.

Dynamic Inference attachments Procedural

Procedural attachments are used to enrich the frames in order to facilitate dynamic inference at runtime. They are tiny programs that are scheduled to run due to some conditions. As an example, a procedure change can be validated or propagated by the if-added procedure in case of the addition of new slot values, whereas the if-needed procedure is followed when a slot value is requested but not found.

Such attachments make frames reactive to do computations, draw conclusions, or retrieve things to the desired point. This process makes the AI system more interactive and flexible. They find wide applications in medical diagnostics, user modeling and robotics, where real-time decision-making is the key.

Frame Systems Chaining Techniques

Although it is the structural knowledge that primarily is represented in terms of frames, they can also engage themselves in inference chaining, i.e., forward and backward chaining. The extent that is forward chaining provides the readily present value of the slots to draw new knowledge (data-driven approach), whereas, in the backward chaining approach, the system has a goal in hand and searches the slots that could assist in the realization of the goal (goal-driven approach). This is to be combined with rule-based systems attached to frames, common in expert systems.

Applications of Frames in AI

NLP Natural Language Processing (NLP)

Frames have large applications in Natural Language Processing in modeling the semantics (meaning) behind sentences through the representation of real-world knowledge and relationships. In the analysis of a sentence, slots in a frame are assigned roles and entities. To take an example of a sentence like, John gave a book to Mary, there could be slots of the frame that the verb, provide, could have where the properties are: Agent = John, Object = Book, and Recipient = Mary.

This aids in semantic role labelling and disambiguation. Frame semantics also assists in systems of dialogue and even question-answer models that connect the language with the context. FrameNet and other similar systems were developed to comprehend better and create human language behaviour with a frame-based approach.

Expert Systems

Expert systems mirroring human decision-making apply frames through domain-specific knowledge. Here, knowledge structures like symptoms, diseases and treatments in such systems are in the form of frames. An example may be a medical diagnosis system where there is a frame called a Patient with such slots as Temperature, Symptoms and Medical History. Such value can give rise to inference rules or procedures to come up with a diagnosis.

With the help of frames, complex data can be structured, organized modularly, and increased as well as decreased with easy-to-update or add to a system. They also enable defaults and derivation so as not to overload the definition of all possible conditions explicitly.

Vision and Robotics Systems

In the case of robotics and computer vision, frames are also significant as they allow structured descriptions of the world, objects, and actions. By way of example, a robot moving about a room could provides a “Room” frame and have slots in it such as; “Dimensions,” “Objects,” and “Lighting.” A frame may be a slot for an Object, e.g., Shape, Position, or Function.

Such frames assist robots in identifying and connecting smartly with their surroundings. Procedural attachments in frames can cause other actions (such as avoiding obstacles or grasping things) when used in combination with sensor input.

Intelligent Tutorial System (ITS)

Frames are provides in education AI systems in the modeling of content as well as student profiles. The examples of slots that can be used in the frame of a student could be: Skill Level, Previous Answers, Learning Preferences. Likewise, in a frame called a lesson, it is possible to have the topics, difficulty level, and related questions. The frames enable intelligent tutoring systems to adapt to each learner through contextualization and giving feedback.

Inference mechanisms or revision materials can anticipate the likely misconceptions that can be recommended. This increases learning and education delivery. Frames, therefore, can be said to be a form of backbone of adaptive learning wherein the learning environment requires a structured but flexible representation of knowledge as well as learners.

Virtual Agents

With game AI and virtual assistant applications, frames are successfully used in modelling the environment, characters, user preferences, and scenarios. As an example, in a role-playing game, a Character frame can include such slots as “Health,” “Inventory,” “Abilities,” and “Goals.” It is possible to update such slots in real-time and make a decision.

Frames express user intents, tasks and current session states in virtual assistants and enable the system to maintain the conversation context and generate context-sensitive responses. Frames combined with procedural attachments assist in making NPCs (Non-Player Characters) and voice-based systems (such as Alexa or Siri) have dynamically networked behaviours, rhetoric or being able to make smart decisions or have intelligent responses.

Scene and Situation Understanding

The frames are very convenient for the representation of situational knowledge or scene-based knowledge when they are used in systems that analyze visually spatial or contextual information. As an example, one surveillance system would have a frame named Scene that would have slots such as Number of People, Object Movements, Time of Day and Unusual Behavior.

With these slots being filled with some sensory information, the system is able to deduce the occurrence of a suspicious activity. Likewise, to make automobiles autonomous, frames contribute to the interpretation of real-time road scenes by organizing input such as road signs, traffic direction, and hindrances. This representation enables reasoning at higher levels, makes decisions and detects events in safety-critical systems.

Artificial Intelligence is a field of data science, and the term artificial intelligence is used because it incorporates intelligence like humans into machines artificially, enabling machines to perform tasks independently without depending on any explicit factors or programming.

Each intelligence is created through complex algorithms and mathematical functions. Artificial intelligence is the practice of making machines so that they can act like humans and make decisions on their own in different situations.

Core Cognitive Functions of Artificial Intelligence

There are three core cognitive functions of artificial intelligence.

1. Generalized Learning
2. Reasoning
3. Problem Solving

Generalized learning

Generalized learning is a cognitive process that allows machines to make and perform the right decisions in different situations or any unexpected situation.

Means to make an accurate prediction on the data for which it has not been trained.

Reasoning

Reasoning in AI is the process of artificial intelligence to make logical conclusions and make informed decisions with the help of available data. It encloses many different types of logical processes, including deductive, inductive, and abductive reasoning, to make accurate predictions, innovative ideas, and responses according to the situation.

Problem solving

Problem-solving in AI is the ability of a machine to identify or analyse a problem, then evaluate the best solution, and then execute a strategy to reach a desired goal, again and again, through the use of mathematical functions, complex algorithms, and search strategies within a defined problem space.

Key Components of Artificial Intelligence

The following are the key components of Artificial Intelligence:

Machine Learning (ML): It is a subset of Artificial Intelligence (AI) that allows machines to learn from large datasets and from past actions without being explicitly programmed. It permits performing tasks like image categorization, data analysis, and fraud detection.

Machine learning is mainly categorised into four types, which are as follows:

• Supervised Learning
• Unsupervised Learning
• Semi-Supervised Learning

Reinforcement Learning: Machines learn by trial and error. They receive feedback. This feedback is in the form of rewards or penalties.

Deep Learning: It is a subset of machine learning. It uses neural networks, and these networks have many layers. This is why it’s called “deep.”

Neural Networks: It is a machine learning system inspired by the functioning of the human brain. It consists of layers of interconnected nodes, and those interconnected nodes are called neurons.

Natural Language Processing (NLP): It is a branch of Artificial Intelligence that learns machines to understand, interpret, and create or generate human language, both written and spoken. It allows computers to understand the meaning of human language and respond in a natural way.

Computer Vision (CV): It is a field of Artificial Intelligence that allows computers to understand and interpret digital images and videos. It extracts data from images and videos, analyzes and classifies them, and provides meaningful insights.

Expert Systems: It is a software of Artificial Intelligence that is used for problem solving and decision making, like a human. User interacts with the system, shares their problem, and acquires an expert system response. I have specific domain knowledge, facts, and rules.

How does Artificial Intelligence (AI) Work?

Understanding of how Artificial Intelligence (AI) functions is essential. We must break down the process. It needs to be broken down into specific stages and mechanisms. At the core, AI mimics human decision-making. This is done with data, algorithms, and Computational power. Let’s get a closer look at how AI functions. We’ll do it step by step:

1. Data Collection

AI systems are learns to perform tasks form data. They need a large amount of data for performing complex tasks, problem-solving, predictions, and to emulate humans for decision-making and critical thinking. So it collects the data from many different sources.

The data can be structured as well as unstructured, such as images, text, numbers, or speech.

2. Data Pre-processing

The data is collected from various sources, which is raw data. It might be useful or a waste, so in data pre-processing, it is cleaned, transformed, and organized. There are key tasks involved in data pre-processing that follow:

Cleaning the data: The cleaning of the data consists of filling missing values, extracting duplicate data, and correcting errors in the data.

• Scaling and Normalization: Scaling adjusted the values of the feature of the collected data to a smaller range. Normalization means changing values commonly with a mean = 0 and a standard deviation = 1.
• Encoding: Converts the categorised data into numerical data, as machine learning models can understand only numbers. Some data can be in text, so convert it into numbers.
• Feature Engineering:Creating, transforming, or extracting new features or details from existing data so the models can learn new things.
• Data Reduction: Sometimes you have unnecessary features (columns) in datasets. So you need to remove data and keep only the necessary relevant data, so it makes it easier and faster to learn models.
• Data Integration: The data is gathered from various sources, like Excel, databases, files, and surroundings. Combine all data into a single dataset so models can easily analyse the data and show a complete picture.

3. Algorithm Selection

There are many algorithms based on different performance, so particularly for machine learning, choosing the most suitable and appropriate algorithm among the options according to machine training is known as algorithm selection.

They are used based on the Task at hand, such as:

1. Linear Regression: This refers to the supervised machine learning algorithm. In this algorithm, it predicts the value of a continuous dependent variable with one or more independent variables as a straight line.
   
2. Decision Trees: A decision tree in AI is a supervised learning algorithm that splits data into branches based on feature conditions to make predictions or classifications based on a hierarchical structure where each internal node represents a decision rule. Each leaf node provides an ultimate result and a classification result.
   
3. Neural Networks: It is a machine learning system inspired by the functioning of the human brain. It consists of layers of interconnected nodes, and those interconnected nodes are called neurons.
   

It learn from data and makes decisions and predictions, allowing it to perform tasks like image recognition and forecasting without explicit programming.

4. Model Training

Model training is the process of learning machines different algorithms repeatedly so they can make productive decisions and perform accurate predictions.

This is considered the training of the model with large datasets to achieve desired outcomes.

5. Model Optimization

Model optimization is the process of improving the performance of a machine or AI model (accuracy of data and predictions, faster response, effective and efficient productivity) in fewer resources, such as power, memory, or computation.

Example

• Hyperparameter tuning → Selection of optimum learning rate, batch size, or the number of layers.
• Regularization → Avoiding overfitting so that the model generalizes well on new data.
• Pruning (in decision trees/neural networks) → Deleting unnecessary branches/nodes.
• Quantization → Lowering precision (e.g., from 32-bit numbers to 8-bit) to lighten models.
• Early stopping →Stop training when accuracy ceases to improve. Inference (Making Predictions).

6. Inference (Making Predictions)

AI inference involves predicting, classifying, or making decisions based on new, previously unseen data, with an AI model that has been trained on existing data. It’s when the AI actually uses the knowledge it has learned to generate real-world outputs, such as by having a photo generator make a new image or a language model take some text and make it into something new. Think of it like the AI “doing” a job after it’s “taught” a skill.

Examples

• Image Recognition: An AI model recognises a cat in a new photograph it has not seen before.
• Natural Language Processing (NLP): A model makes personalized show recommendations on Netflix based on a user’s viewing history, or it auto-completes the next word in an email message.
• Self-Driving Car: An autonomous vehicle, such as a self-driving car, leverages inference to perceive road signs and to move through challenging road scenarios.

Types of Inference

• Batch Inference: It processes a large batch of data at once and makes predictions offline.
• Online Inference: With each request, predictions are produced immediately, and response time is real-time.
• Streaming Inference: A streaming pipeline processes data as it comes in for predictions.

7. Deployment

AI model deployment is the last step of putting a trained machine learning model into a production environment, where it can make accurate predictions and create value for users or systems. Deployment is where the models are captured, put into an application, and the predictions can be assessed through an API.

Deployment has unique challenges, including operational needs or scalability, reliability, and security once deployed into production, and lastly, the need to monitor the model because it may fail or degrade in performance and need to be retrained.

Deployment is a transition of a trained AI model that is being moved from a development environment to a live environment, where it can make predictions based on new data and return those outputs.

• The goal is to make the capabilities of the model accessible to end-users, applications, or other systems, thereby being able to automate decisions or tasks.
• This is a significant step in getting tangible AI to come to value, whether that is fraud detection, patient risk prediction, or face recognition.

Applications of Artificial Intelligence

The following is a list of applications of artificial intelligence:

• Healthcare: AI is used in diagnosing diseases. It is also used in personalizing treatment plans. AI is even used in drug discovery.
• Finance: AI is helpful in fraud detection. It is also helpful in credit scoring. Algorithmic trading is another Area AI aids in. Customer service chatbots also have a Role where AI plays.
• Transportation: Autonomous vehicles like self-driving cars need AI to navigate. They also use AI to make real-time decisions.
• Retail: AI enhances recommendation engines. It is useful in Customer segmentation, too. AI also improves inventory management systems.
• Entertainment: AI offers personalized Content recommendations. Platforms like Netflix and YouTube benefit from this technology.

AI is no longer the buzzword that we used to hear. It is a fast-evolving technology that has now become a part of our lives. It is changing the way we live, work, and the way we interact with the world. AI has found its way from voice assistant to self-driving car. It is truly an inevitable part of modern life, and to understand the workings of AI, we also need to tour its core domains.

The different areas in which intelligent behavior is created and used are represented by the domains of artificial intelligence. Computer vision, robotics, expert systems, machine learning, and natural language processing are a few of these domains. Each domain contributes in a different way to enabling machines to see the world, comprehend human language, learn from facts, and make judgments.

Machine Learning

Machine Learning (ML) is a subset of AI that aims to create computers that can improve their performance from the data that they collect with little human guidance. This has made it a must-have tool in different industries, depending on its capabilities of processing large data sets and identifying patterns that probably could not be easily seen by the naked eye. Machine learning comprises different methods of learning that are grouped using different categories. Below, we delve into the primary types of machine learning: The machine learning techniques discussed include supervised learning, unsupervised learning, reinforcement learning, and deep learning, as well as the usage of each of them in various fields.

Supervised Learning

Supervised learning is a subset of the overall machine learning pattern, in which the model is trained using data that is already labeled. This means that each training example that is given shall be followed by only one output label. Supervised learning is beneficial in producing a mapping function that will help estimate the labels of unseen data.

Types of Supervised Learning:

• Regression: The objective of regression-type algorithms is to make predictions on continuous values. Some of the algorithms that are commonly used include Linear Regression, Decision Trees, and Support Vector Machines (SVMs), among others. For instance, predicting the price of a house given characteristics such as size, area, and the number of bedrooms, among others.
• Classification: The task of classification calls for predicting specific categories, for example, whether an email is spam or not spam. They frequently use algorithms such as logistic regression, random forest, and neural networks.

Training Process:

• Supervised learning is the process whereby the model is fed a dataset of input and output examples. This causes the model to change parameters with a view to reducing the discrepancy between the test data and labels. Some methods used include backpropagation, a technique used to adjust the weights of a model in neural networks.

Evaluation Metrics:

• Accuracy: It is the number of instances predicted correctly to the total number of instances of that class.
• Precision and Recall: Precision, on the other hand, calculates the number of correct positive predictions, while recall is the hallmark of a good classifier: it can identify all related instances.
• F1 Score: A single value for the precision and the recall that averages the two values to try to find a middle value.

Unsupervised Learning

Unsupervised learning relates to the deployment of data labeled without guidance as the model is trained. In this process, the model’s goal is to identify underlying patterns or structures within the data. Such a type of learning is applicable when there is a limited amount of labeled data or when the interest is in the structure of the data itself.

Types of Unsupervised Learning:

• Clustering: Clustering involves bringing together elements recognized as similar to make up a group. Some of the frequently used clustering algorithms are K-Means clustering, Hierarchical clustering, and DBSCAN. Their uses include customer analytics and image storage and manipulation.
• Association: The association helps to discover interesting relationships between variables in large data sets. Market basket analysis, where items bought together are recognized, is a good example.

Applications:

• Anomaly Detection: Anomaly Detection is the process of detecting things that are out of the ordinary or characteristic of a system that is different from what is considered normal. It is used mostly in fraud detection, network security, and fault detection.
• Dimensionality Reduction: Algorithms such as PCA and t-SNE are dimensionality reduction procedures that attempt to help visualize large datasets and improve efficiency.

Reinforcement Learning

Reinforcement Learning (RL) is a learning paradigm in which people interact with an environment to make decisions. The agent gets a reinforcement in the form of a bonus or penalty and seeks to acquire the maximum number of bonuses over an indefinite time.

Components of Reinforcement Learning:

• Agent: The one that communicates with all the factors in the environment in the process of decision-making.
• Environment: The context of the agents’ operation, which is a state, actions, and reward system.
• Policy: The agent uses this technique to determine which state to take the following action.
• Reward Function: A loop that is used to review the activities performed by the agent.

Popular Algorithms:

• Q-Learning: An algorithm that uses the policy of another controller but learns action-state values.
• Deep Q-Networks (DQN): Extends Q-Learning by introducing deep neural networks to address large-scale, complex environments.
• Policy Gradient Methods: These methods directly learn the policy parameters so as to make more flexible decisions.

Applications:

• Game Playing: RL has been able to attain a level past that of human intelligence, especially in games such as Chess, Go, and Atari, through aspects such as AlphaGo and Deep Q-Network.
• Robotics: Training robots to accomplish simple actions in daily scenarios like manipulation and avoiding, or going around obstacles.
• Autonomous Vehicles: RL is applied to build navigation systems that modify routes and train the vehicle on how to operate under current traffic conditions.

Deep Learning

Deep learning is one of the branches of machine learning, which is known as the learning process that uses neural networks with multiple layers. It has transformed fields such as computer vision, natural language processing, and speech recognition.

Structure of Neural Networks:

• Input Layer: This is the receipt of input data.
• Hidden Layers: Intermediate layers that capture the net’s inputs and code them to extract features that will benefit the network’s classification tasks.
• Output Layer: This is the final output of the model that generally provides the prediction or classification.

Types of Neural Networks:

• Convolutional Neural Networks (CNNs): This focus has been on the image processing feature to recognize spatial hierarchies with the help of convolutional layers.
• Recurrent Neural Networks (RNNs): Due to their design for sequential data, RNNs are used in language models and time series analysis.
• Generative Adversarial Networks (GANs): Consisting of two networks (generator and discriminator), GANs produce real and new data points, such as image or signal data.

Training Deep Neural Networks:

• Backpropagation: A technique that aims to adjust the weights of the network in relation to an error rate that is arrived at in the previous epoch.
• Optimization Algorithms: Algorithms like Stochastic Gradient Descent (SGD) and Adam are employed to optimize the model; that is, to minimize the loss function.
• Regularization Techniques: These techniques, such as dropout and batch normalization, help reduce the cases of overfitting and increase the generality of a model.

Applications:

• Image and Video Analysis: Applications that use deep learning include facial recognition, object detection, and video tagging.
• Natural Language Processing (NLP): Applied in contexts of language translation, analysis of the sentiment of the text, and chatbots.
• Healthcare: Helping in the disease diagnosis based on medical images and the prognosis of the outcomes of a patient.

Computer Vision

Image Recognition

Image recognition can be easily said to be the first tool in the field of Computer Vision. It includes recognizing things, locations, people, and events in a particular picture.

How does it work?

Image recognition is mostly dependent on deep learning neural networks, specifically CNNs, which are used to process topological data, including images. These algorithms train themselves to recognize patterns and derive new, accurate classes from a very large set of images, where the images are labeled and initial weights in the network are adjusted to minimize the error of classification.

• Data Processing: First, the image is quantized and turned into a set of numbers that the computer can understand. This entails pixel intensity as well as other feature extraction.
• Model Training: The model uses learning through a labeled dataset in which each image is provided with the right label or category. This enables the network to learn the features that distinguish one class from the other.
• Feature Extraction: CNNs learn features by going through layers of convolutions and pooling to discern specific features in the objects within the images.
• Classification: After training, the model is capable of sorting new images into the given classes with a high degree of precision.

Applications:

• Healthcare: We diagnose diseases from pictures and images, such as X-rays, MRI scans, and CT scans, where we locate tumors, fractures, etc.
• Retail: Improve shot satisfaction by identifying products and delivering recommendations for customers utilizing information provided in the shots.
• Social Media: Examples of applications include automatically tagging friends in photos and blocking/filtering content considered unsuitable by friends.

Object Detection

Object detection is one level more complex than image recognition because, in addition to identifying objects in the picture, it highlights their position with a rectangular box.

How does it Work?

We mentioned earlier that object detection is closely related to classification and localization. The algorithm detects an object in the image and returns the coordinates, which makes it easier to define the object in an image.

• Bounding Box Creation: The modeling output is the locations of the bounding box that encases objects in that picture.
• Classification and Localization: Alongside defines what the object is and where it could be found.
• Non-Maximum Suppression: Reduces the number of entire boxes and chooses the most likely ones to enhance accuracy.
• Training: There is a variety of approaches to real-time object detection, among which YOLO (You Only Look Once) and SSD (Single Shot MultiBox Detector) are widely used.

Applications:

• Autonomous Vehicles: Identifying both the pedestrian and vehicle, as well as the obstacles in the way to avoid being involved in an accident.
• Security Systems: Monitoring or detecting anyone who is an unauthorized person or engaging in suspicious activity within restricted areas.
• Wildlife Monitoring: Inventory and estimate wild animals in their natural habitats for their protection.

Facial Recognition

Biometrics involves using facial detectors to identify and authenticate a person based on his/her facial structure. It has especially become relevant in the realms of security and individualization, among other things.

How does it work?

The facial recognition system measures the facial attributes, translates them into a faceprint, and stores them in its database. The following steps are crucial in facial recognition:

• Face Detection: Face Detection Involves Recognising people’s faces, normally using algorithms such as Haar cascades or MTCNN (Multi-task Cascaded Convolutional Networks).
• Feature Extraction: This would include features like the distance between the eyes, the shape and size of the nose, the jawline, etc.
• Comparison and Matching: To find a match, match the extracted features with those of faces stored in a database.
• Verification: The previous stage of comparing the similarity of the names of the person with those in a database of known individuals to confirm their identity.

Video Analysis

Video surveillance includes the identification and evaluation of phenomena within a video. Given its real-time nature, it has become an important technology in many fields.

How does it work?

The extraction of this specific video content is done using computer vision methods such as motion detection, object tracking, and scene recognition.

• Frame-by-Frame Analysis: Scribbling across the frames to note transitions and to recognize objects in motion.
• Object Tracking: Indeed, this could be done by tracking detected objects through different frames, aiming to analyze subsequent actions and cooperation.
• Event Detection: Involves specific events, such as a car accident or a person entering a restricted area.
• Real-Time Processing: This involves employing algorithms that offer the capacity to analyze the video content feed in real-time for immediate results.

Applications:

• Traffic Monitoring: Traffic Monitoring involves identifying hotspots, that is, congestions or accidents that may have occurred on roads to enhance traffic flow.
• Sports Analytics: Involves unlocking the patterns of player movement and making necessary improvements in the game plan to affect a team’s performance.
• Retail: Customer activity analysis and store environment organization according to people’s movement schemes.

Augmented Reality

Augmented Reality (AR) combines the real and virtual worlds where digital information is placed on top of the real environment. Computer vision is a core technology in AR because it allows augmented objects to be incorporated into live scenes.

How does it work?

AR also employs machine vision to make sense of the environment, tangibly integrating the virtual with the physical setting.

• Environmental Understanding: It computes a map of the environment using a technique known as Simultaneous Localization and Mapping, abbreviated as SLAM.
• Feature Detection: Localization is a process of finding points or areas where digital objects can be placed.
• Interaction: Allowing to touch or manipulate, or in other words, make virtual objects interact with the physical environment of an ML.
• Rendering: Integrated real-time interaction between the virtual and real domains with great accuracy.

Applications:

• Gaming: Infusing part of the real physical environment into the game improves realism, and creativity in gameplay.
• Education: Augmenting Education through the means of placing educational content over real-life objects.
• Retail: Enabling the customers to see almost all the products inside their homes before making a purchase.

Artificial General Intelligence (AGI)

The term Artificial General Intelligence (AGI) is an element of artificial intelligence that focuses on designing machines that can become wise in every aspect of the mental procedures a human being can solve. Narrow AI is very good at particular activities, such as language translation or image recognition, while AGI aspires to comprehensive intelligence.

Definition and Current Status

Definition:

Artificial General Intelligence (AGI) describes the capability of a machine to solve any problem that a human brain is capable of solving. This form of intelligence refers to intelligence that extends beyond the current problems and is capable of transferring knowledge from one area to another. This capability includes issues of reasoning and solving as well as the application of emotions and even the ability to sense, in the broadest meaning of the term.

Current Status:

AGI remains largely theoretical. Today’s AI examples are representatives of ”narrow AI,” which is aimed at solving only slightly divergent problems and does not extend into different fields. Despite all the AI developments, true Artificial General Intelligence has yet to be developed.

• Technological Limitations: Contemporary SQ systems are based on complicated algorithms designed to solve explicit problems. They do not possess the ability to learn and pass knowledge to other sectors or areas as the human brain does. For example, AI that translates from one language to another cannot change this task to solve mathematical issues unless the program is designed to do so.
• Research Initiatives: AGI is currently a hot topic in the industry; most major companies and research laboratories, such as OpenAI and DeepMind, are heavily involved in AGI research. This path considers some approaches, which include neural networks, cognitive architectures and transfer learning, to achieve an AI with general intelligence.
• Timeline Uncertainty: Opinions about when AGI will be achieved differ from each other, as do the time frames experts give for it. Some theorists have predicted that it may occur within a few decades, while others have pointed out that it may take a long time or, at times, might not be possible at all. The challenge of performing similar tasks to the human brain also prevents a clear timeline for the creation of an AGI.

Research Directions

Approaches and Theoretical Models:

• Neural Networks and Deep Learning: These models try to mimic the brain’s abilities, structure, and learning methods. AI automation has produced innovations that can work like humans and make decisions, but these automations are not well generalized.
• Cognitive Architectures: Scholars are working on other cognitive architectures, such as ACT-R and SOAR, to model human cognition. These frameworks attempt to mimic behavior that involves memory, learning or even decision-making, which can provide some understanding of how AGI may be designed.
• Transfer Learning: This approach mainly concerns the ability of a machine to transfer knowledge from one domain to another related domain. It is a move towards AGI; it enables systems to become more general, less rigid and less naive and does not have to be trained on a specific task in order to perform well on it.
• Meta-Learning: Meta-learning is also often described as ‘learning to learn,’ a process that is structurally similar to the development of better strategies for solving a particular problem over time similar to how human beings do.
• Neuromorphic Computing: Neuromorphic computing focuses on creating electronics and computational models similar to the brain. Thus, by creating systems similar to the human brain, scientists are likely to design more flexible and effective AI.

Interdisciplinary Collaboration:

• Neuroscience: Knowledge of the brain helps people implement AI and, thus, conceive AGI. By analyzing brain functioning, researchers may create more effective models of human thinking.
• Psychology: Understanding human behavior, learning processes, and feelings contributes to the development of models of AGI that are not only intelligent but also aware of human behavior.
• Ethics and Philosophy: It is evident that as AGI becomes even closer to being realized in the future, philosophical issues such as consciousness, rights, and moral status will be as well. Some measures that revolve around ethical standards help in the establishment and deployment of AGI.
• Computer Science and Mathematics: Algorithmic improvements, hardware, AI/ML techniques, and the ability to leverage formalisms in mathematics are central to AGI advancement.

Foundation Models and Generative AI

Driven by large-scale foundation models like GPT (by OpenAI), Gemini (by Google), and Claude (by Anthropic), generative artificial intelligence is changing how AI is used in many different fields. With little input, these models can generate video material, audio, images, human-like text, and code. This is inspiring creativity in scientific research, education, software development, content generation, and even more.

Applications

Virtual assistance, legal drafting, marketing content, automated coding, creative writing, and personalized tutoring.

Edge AI

TinyML and Edge AI are major changes in how artificial intelligence is used and deployed. Traditionally, AI models needed strong cloud servers to process data and make decisions, sometimes causing latency, increased energy use, and possible privacy issues. Edge AI alters this by allowing AI computations to take place directly on local devices, such as smartphones, smart cameras, wearables, or embedded systems, without depending on continuous internet connectivity.

This strategy guarantees quicker reactions, improved data privacy, and lower bandwidth consumption. Complementing Edge AI is TinyML (Tiny Machine Learning), which runs machine learning models on ultra-low-power microcontrollers and embedded systems. Though tiny and underpowered, these devices can quickly do real-time analysis and decision-making.

Applications

In sectors like healthcare (e.g., patient monitoring devices), agriculture (e.g., soil moisture sensors), smart homes, and industrial IoT, where immediate, localized intelligence is crucial, applications of Edge AI and TinyML are proliferating. With little resource use, these technologies are opening the path for more responsive, smarter environments.

XAI

By explainable AI, we mean techniques and methods employed in making the decisions of AI systems more transparent, understandable, and interpretable to humans. With the advancement of AI models, especially complex ones like deep learning or ensemble methods, they become increasingly powerful and have a tendency to become “black boxes.”

How does it work?

In such models, the internal workings and logic behind predictions would be hard to understand. This is often a big issue in critical fields like health, finance, law, and autonomous systems, where understanding the reason behind a decision made by an AI model is as crucial as making that decision itself.

XAI addresses this concern by the means of understanding how models process data, weigh features in their importance, and thus reach conclusions. Methods like SHAP (Shapley Additive exPlanations), LIME (Local Interpretable Model-agnostic Explanations), and attention mechanisms contribute to visualizing or pointing out what aspects mattered in the outcome of the model.

In fact, explainable AI will help create trust and responsibility within users, and will further assist in their diagnostics, fairness and bias reduction, and conforming to legal and ethical standards, such as GDPR. Eventually, as AI creeps more into everyday lives, XAI will become a major partner in making intelligent systems all the more transparent, ethical, and user-friendly.

NeuroSymbolic AI

The new wave of artificial intelligence, neurosymbolic and hybrid models, brings the power of symbolic reasoning and neural-network-based learning together. Classical symbols-logic, rules, and structured representations-are forms of AI that attempt to simulate human reasoning and are highly interpretable and effective with explicit knowledge tasks such as mathematics and legal reasoning.

Neural Networks (especially deep learning models) use these capabilities to analyze unstructured data such as images, texts, and audio. However, they are treated and operate as black boxes with very limited interpretability. Neurosymbolic AI is meant to fuse the pattern-recognizing facilities of the first with the rule-based, logical reasoning properties of the second.

Why NeuroSymbolic AI?

Neurosymbolic AI applies to a wider range of tasks requiring both learning from data and applying logical rules to tasks more naturally human-like and contextual in reasoning. Such hybrid models are thriving in complex application fields such as scientific discovery, where it is both imperative to have the facility of data-dedication, and in autonomous systems, robotics, and natural language understanding.

Combining learning with reasoning, neurosymbolic AI can thus be expected to give stronger, generalizable, explainable AI, which would adapt to new scenarios while keeping consistency with established knowledge.

Autonomous System

Autonomous Systems and Robotics have become very active fields of artificial intelligence, where they allow machines to sense, decide, and act on their own with minimal or no human intervention. These systems are being spread to a number of various parts such as manufacturing, logistics, agriculture, healthcare, and personal assistance.

Current Status

This development is a field of electronics: robotics, which is defined as mechanical systems fitted with sensors, actuators, and intelligent control algorithms, allowing the system to operate in reality. Current autonomous robots tend to be built on reinforcement learning principles, where robots learn the behavior they should exhibit through interaction with their environment while being given feedback in real-time.

Their visual and language input capability enables visual interpretations and the understanding of natural language commands, especially in terms of the human-robot relationship. Companies such as Boston Dynamics have built very agile field robots like Spot and Atlas, which can ply very difficult terrains and do physical tasks. On the other hand, Optimus from Tesla is still in the process of being conceived as a humanoid robot that would be capable of performing tasks in semi-structured environments, such as homes or factories, in pursuit of being useful for almost in general purposes.

Conclusion

In conclusion, it is crucial to note that the domains of artificial intelligence comprise quite a vast field of applications implemented in and across various spheres of human life and industries. Starting from natural language processing and Robotics, Computer vision, and expert systems, all the domains provide potential features that can enrich productivity, effectiveness, and creativity.

Those are the AI domains that are changing the ways people communicate with technology and the ways companies function, advancing healthcare solutions, finances, entertainment, and much more. Thus, with the development of AI, its domains will grow even wider, which will lead to new possibilities and prospects that will define the further development of autonomous technologies and their impact on people’s lives.

This topic discusses the definition of both Artificial Intelligence (AI) and Human Intelligence (HI) and differentiates them. AI and HI are two such ideas that are likely to be compared and contrasted. AI is a field that is concerned with designing machines or computer programs to do things that can be described as intelligent for instance, learning, comprehension, planning, perceiving, etc. Human intelligence is defined as the mental abilities of people and their capability to think alike.

What is Artificial Intelligence?

Artificial Intelligence is an intellectual system imitating in the solution of matters typically done by human intelligence. This machine employs machine learning approaches and methods that help in determining decisions from large datasets. The domains in which artificial intelligence is applied are the Media domain, the healthcare domain, and many more.

Decision-making by artificial intelligence systems is actually the copying of certain kinds of activity with respect to the usage in robotics. This essay will show that most people do not realize how influenced their lives are with AI-powered systems at present. Some examples include autocorrect, face recognition, smart speakers, Google Maps, and among others, AI has an incredible feature of self-diagnostic, self-training, and self-correcting mechanism with negligible or no human interjection.

What is Human Intelligence?

Human intelligence may be defined as a capability that allows individuals to acquire knowledge from experience, be flexible, think in a sophisticated manner, and use acquired knowledge to make decisions. These factors entail characteristics such as thinking, solving problems, comprehending language, innovating, and regulating emotions. Both our genes and the environment around us shape our intelligence. It also increases as children gain knowledge, relate with others, and encounter other cultures.

Differences Between Artificial Intelligence Vs. Human Intelligence

The main way that human beings can differ is through the flexibility and innovation of Human Intelligence. On the other hand, the following qualities are aspects that cannot be embedded in an AI model: abstract thinking, adapting to new environments, and finding innovative ways of adapting to change. Other areas where humanness is most evident and where people can relate include emotional intelligence, empathy, intuition, and interpersonal skills through which people can relate and interact right from the workplace in terms of cooperation and information sharing.

Three significant fields where AI performs exceptionally well are vast scale data processing, quick and accurately categorized data processing, and doing any kind of repetitive job at its best. It is outstanding when it comes to its capacity for pattern recognition, further to the assessment of probable outcomes, and last but not least, in its ability of sound decision-making that is grounded on extensive and comprehensive data processing.

In some sectors, such as health, finance, and transportation, AI operates very fast and efficiently, and there is a lot of increase in productivity. The areas of concern are that it is not capable of understanding some things or will not be creative as well, as it has no ’emotional intelligence’. It operates within certain parameters and does not incorporate reason or what may be deemed ethical.

Listed below are some of the central differences between human and artificial intelligence:

Element	Human Intelligence	Artificial Intelligence
Nature	Biological, Natural Computes	Synthetic
Learning Method	Experience-based, intuitive, and emotional	Data-driven, Algorithms, and predefined rules
Adaptability	Chaotically adaptive and can handle novelty and unpredictability	Poor adaptability; excels in specific, pre-defined tasks
Creativity	Chaotically creative, highly able to think abstractly, and innovate	Poor creativity; can only pattern mimic, lacks innovation
Decision-Making	Emotionally, ethically, and socially driven	Based purely on data, logic, and parameters set
Speed	Slower, biologically limited	Extremely fast, computing power dependent
Generalization	Good at generalizing knowledge across different domains	Poor at generalization; often task-specific
Energy Consumption	Low, around 20W for the human brain	High, depending on task complexity and hardware
Communication	Complex language, emotions,	Limited to pre-defined language models and interfaces
Learning Capacity	Lifelong, able to learn continuously and dynamically	Requires retraining and update of models, not lifelong
Problem-Solving	Both Logical and Emotional Reasoning	Rules base and pattern-dependent
Error Handling	Emotionally intuitive	Can learn from errors by retraining or adjusting the algorithms.
Consciousness	Self-aware, has consciousness, and experiences subjectivity	No consciousness and self-awareness
Ethics and Morality	Driven by cultural, social, and personal values	No inherent ethics, ethics are formed and constrained by code
Resourcefulness	Very resourceful in inventing new ways of solving problems	Resourcefulness is limited to its programming and data.

Human Creativity vs. AI Efficiency

While AI is unbeatable in efficiency, human intelligence has no equivalent for creativity. Creativity describes the act of coming up with new ideas, thinking “outside the box,” or creating some original work of art or literature, for instance, coming up with a solution to some problem. However, human creativity is greatly inflamed by emotions, cultural background, and personal experience.

AI is also helpful in bringing out creativity: it gives inspiration, variation of ideas on a theme, or even in the automation of some creative work. For instance, it may be an AI algorithm generating music or art following the patterns that are learned from existing works. However, those creations usually lack the depth, meanings, and emotional resonance that come from human creativity. Perhaps what truly distinguishes humans from artificial intelligence is the ability for humans to create something entirely new, born out of imagination and fueled by personal experience.

Conclusion

Both Artificial Intelligence (AI) and Human Intelligence (HI) include a lot of similarities. However, AI systems have the capacity to execute the activities that need to be done with human intelligence but without emotion, imagination power, cannot think on their feet or have the emotional intelligence that humans have.

Like any other intelligent element in our human body, Human Intelligence is a combination of genes, environment, and experience that empowers our human beings to intelligently understand and navigate through the environment, whereas AI fails to do so. With the development of AI, it is essential that we understand the differences between AI and Human Intelligence.

Artificial Intelligence is basically understood as one of the fundamentals in the current technology that is inclusive in various domains, including healthcare, finance, transport and entertainment. It advances very quickly and is beginning to be used at many of the places where machines learn and analyze data.

AI technologies that are part of human life help human beings in complex data processing and make maximum available help to a person in his personal life. As such, AI technologies will be used more and more in our lives and give us smarter solutions, better predictions, and smarter decision-making in more and more areas.

Importance of artificial intelligence

The significance of artificial intelligence and its succeeding elements have been recognized for a long time. They are viewed as methods and instruments to improve the world. It is significant because it simplifies our life. Humans greatly benefit from these technologies, which are designed to need as little human labor as feasible. They are capable of automated operation. As a result, the final thing that is observed while using this technology is human involvement.

These devices are a helpful tool that expedites your chores and procedures with assured accuracy and precision. With their easy and common methods, these technologies and apps not only make the world a mistake-free place, but they also have uses outside our daily lives. It has an impact on and significance for other fields as well.

Top Uses of Artificial Intelligence

In Medical Science

The medical business has seen a significant transformation due to artificial intelligence (AI). A number of important use cases, including identifying whether a given patient has benign or malignant cancer or tumor according to the symptoms, medical data, and history, have been effectively predicted using a variety of machine learning algorithms and models. In future forecasts, it is also utilized to caution patients about their declining health and the steps they need to take to resume a normal and healthy life.

An AI-powered virtual care assistant has been developed especially to meet the demands of individuals. Monitoring, researching various cases, and analyzing previous instances and their results are all common uses for it. Additionally, it aims to increase the productivity of its helpers and models by anticipating areas for improvement and developing their intelligence.

Healthcare bots, which are known to offer round-the-clock support and handle the less crucial task of scheduling appointments, are another effective strategy used by the medical business to advance in the field.

In the Field of Air Transport

Air transport is one of the major systematic transports in the world, and the need to optimize the operation of their mode of operations has now become urgent. Artificial Intelligence got involved here, and the machine, along with the flight landing and take-off charts, plans routes.

Many aircraft and navigation maps, taxing routes, and a quick look over the whole cockpit panel (to make sure every component was operating correctly) were already employing artificial intelligence. It gives too promising results and hence has been widely adopted. Air transport Artificial intelligence in the ultimate aim is to make it easier and more comfortable for human beings to travel.

In the Field of Banking and Financial Institutions

Artificial Intelligence helps in managing financial transactions and many other activities in the bank. Machine learning models are making bank operations, such as transactions, financial operations, stock market money, and their management, among others, easier and more efficient.

For example, anti-money laundering is a classic banking or financial industry use case where artificial intelligence is being used for monitoring and reporting suspicious financial transactions to regulators. For example, credit card companies also use it for credit systems analysis. Credit card transactions on suspects are tracked internationally and acted on and resolved based on different parameters.

In the Field of Gaming and Entertainment

Artificial intelligence has made a huge leap forward in one industry above all others: from virtual reality games to modern games. You don’t need another person to play and bots are always available for you to play with.

Also with the advent of Artificial Intelligence comes the possibility of highly personalized detail and graphics that are taking this industry to another level.

AI Achieves Unprecedented Accuracy

Deep neural networks are the backbone using which AI has achieved the otherwise impossible accuracy.

Google Search and your interaction with Alexa are all deep learning to date, examples of which are increasingly getting more accurate as they learn more through your daily use of them. Medical fields use AI techniques to search for cancer cells on MRI with high precision from highly trained radiologists.

AI Is Reliable & Quick

The computer performs computer-generated tasks consistently, extensively, and consistently. But you need humans to set it all up, humans to ask the right questions.

AI Adds Intelligence to Products

AI isn’t going to be a product that you are going to buy. The contrary side is that your products will be boosted with AI integration, like it’s been presented in the case of Apple products with the Siri feature.

Many technologies in our homes and workplaces can be improved using chatbots, automation, smart devices, and huge quantities of data.

AI Evaluates Deep Data

Big data and computing power make fraud detection systems possible that were practically impossible just a few years ago.

Deep learning models learn directly from the data, and so you need lots of data to train them. The more data, the more accurate they are.

Conclusion

Artificial Intelligence is growing at an exponential rate in applications of the expansive needs-fulfilling sectors. It has become the reason for the productivity and precision increased. It helps us learn from data, adapt to new conditions, and handle tens of the messy bits of our modern life. AI has done a lot in healthcare, if not more, and transformed modes of transportation, which are continuing to advance and transform the finance and entertainment industries.

Technology will grow, and it will be in the form that will continue to grow to help us provide greater solutions for life’s norms. The adoption of AI is not just about unfolding the opportunities ahead but about being able to adapt to a new world where people and AI are both supposed to do important things.

Undoubtedly, Artificial Intelligence (AI) is a revolutionary field of computer science, which is ready to become the main component of various emerging technologies like big data, robotics, and IoT. It will continue to act as a technological innovator in the coming years. In just a few years, AI has become a reality from fantasy. Machines that help humans with intelligence are not just in sci-fi movies but also in the real world. At this time, we live in a world of Artificial Intelligence that was just a story though for some years.

We are using AI technology in our daily lives, either unknowingly or knowingly, and somewhere it has become a part of our lives. Ranging from Alexa/Siri to Chatbots, everyone is carrying AI in their daily routine. The development and evolution of this technology are happening at a rapid pace. However, it was not as smooth and easy as it seemed to us. It has taken several years and lots of hard work & contributions of various people to take AI to this stage.

Being so revolutionary technology, AI also deals with many controversies about its future and impact on Human beings. It may be dangerous, but also a great opportunity. AI will be deployed to enhance both defensive and offensive cyber operations. Additionally, new means of cyberattacks will be invented to take advantage of particular vulnerabilities of AI technology.

This topic will discuss the future of AI and its impact on human life, i.e., whether it is a great technology or a threat to humans.

Artificial Intelligence (AI) at Present

Before going deep dive into AI in future, first, let’s understand what is Artificial Intelligence and at what stage it is at present. We can define AI as, “It is the ability of machines or computer-controlled robot to perform task that are associated with intelligence.” So, AI is computer science, which aims to develop intelligent machines that can mimic human behaviour.

It is clear we are in the era of Narrow or Weak AI, when very sophisticated algorithms or AI models perform well in a specific situation or job, such as AI assistants, such as ChatGPT, Gemini, and self-driving cars utilizing object recognition. Even if we have gradually integrated those applications into our daily lives, the course of AI development is defining two major seinents: Artificial General Intelligence (AGI), with human-level cognition through reasoning, and at the zenith, Super AI, with intelligence transcending human beings in all domains.

Based on capabilities, AI can be divided into three types that are:

• Narrow AI: It is capable of completing dedicated tasks with intelligence. The current stage of AI is narrow AI.
• General AI: Artificial General Intelligence or AGI defines the machines that can show human intelligence.
• Super AI: Super AI refers to self-aware AI with cognitive abilities that surpass that of humans. It is a level where machines can do any task that a human can do with cognitive properties.

At the current stage, AI is known as Narrow AI or Weak AI, which can only perform dedicated tasks. For example, self-driving cars, speech recognition, etc.

Myths about Advanced Artificial Intelligence

1. Superintelligence by the year 2100 is not possible.

The reality about the possibility of superintelligence is that currently, we can’t determine it. It may occur in decades, or centuries, or may never, but nothing is confirmed. There have been several surveys in which AI researchers have been asked how many years from now they think we will have human-scale AI with at least a 50% chance. All of these surveys have the same conclusion: The world’s leading experts disagree, so we don’t know. For example, in such a survey of AI researchers at the 2015 Puerto Rico AI conference, the (average) answer was by 2045, but some researchers estimated hundreds of years or more.

2. AI will Replace all human jobs.

It’s certainly true that the advent of AI and automation has the potential to disrupt labour seriously – and in many situations, it is already doing just that. However, seeing this as a straightforward transfer of labour from humans to machines is a vast oversimplification.

With the development of AI, a revolution has come in industries of every sector, and people fear losing their jobs with the increased development of AI. But in reality, AI has come up with more jobs and opportunities for people in every sector. Every machine needs a human being to operate it. However, AI has taken over some roles, but it has reverted to producing more jobs for people.

3. Computers will become better than Humans

As discussed above, AI can be divided into three types: Weak AI, which can perform specific tasks, such as weather Prediction. General AI: Capable of performing tasks that humans can do, Super AI: AI capable of performing any task better than humans.

At present, we are using weak AI that performs a particular task and improves its performance. On the other hand, general AI and Super AI are not yet developed, and research is going on. They will be capable of doing different tasks similar to human intelligence. However, the development of such AI is far away, and it will take years or centuries to create such AI applications. Moreover, the efficiency of such AI, whether it will be better than humans, is not predictable at the current stage.

4. AI does not require human intervention.

People also have a misconception that AI does not need any human intervention. But the fact is that AI is not yet developed to make its own decisions. A machine learning engineer/specialist is required to pre-process the data, prepare the models, prepare a training dataset, identify the bias and variance, and eliminate them etc. Each AI model is still dependent on humans. However, once the model is prepared, it improves its performance on its own from the experiences.

5. AI does not have a Human Component

Every phase in the life cycle of an artificial intelligence (AI) has a human touch, contrary to a generally accepted belief about AI independence. Human experience is evident at every phase, from data preprocessing all the way through model development, and then some continuous model evaluation and adjusting.

Human input is vital to guarantee that AI systems are valid, fair, and dependable. While AI technologies may develop over time depending on data, a particular drawback of these systems is also the quality of the data, as well as any possible prejudice. A person can lower the possibility of negative results.

How can Artificial Intelligence be risky?

Most of the researchers agree that super AI cannot show human emotions such as Love, hate, or kindness. Moreover, we should not expect an AI to become intentionally generous or spiteful. Further, if we talk about AI being risky, there can be mainly two scenarios, which are:

1. AI is programmed to do something destructive

Autonomous weapons are artificial intelligence systems that are programmed to kill. In the hands of the wrong person, these weapons could easily cause mass casualties. Moreover, an AI arms race could inadvertently lead to an AI war resulting in mass casualties. To avoid being dissatisfied with the enemy, these weapons would be designed to be extremely difficult to “turn off,” so humans could plausibly lose control of such a situation. This risk is present even with narrow AI but grows as levels of AI intelligence and autonomy increase.

2. Misalignment between our goals and machines

The second possibility of AI as a risky technology is that if intelligent AI is designed to do something beneficial, it develops destructive results. For example, suppose we ask the self-driving car to “take us to our destination as fast as possible.” The machine will immediately follow our instructions.

It may be dangerous to human lives until we specify that traffic rules should also be followed, and we value human life. It may break traffic rules or meet with an accident, which was not really what we wanted, but it did what we asked it to. So, super-intelligent machines can be destructive if they attempt to accomplish a goal that doesn’t meet our requirements.

3. AI Taking Control over Art

Furthermore, intelligent tools have permanently altered the processes by which digital art and images are produced. Users may then create even very realistic and creative images in any style thanks to text prompts. For instance, Midjourney makes artistic-and often surreal-photos more readily available to regular consumers; those without art expertise may now create visual prompts from their fantasies. Graphic design, illustration, and other personal expressions on social media directly benefit from this development.

4. AI taking over Blogs

AI models mimic human-text behavior and take material freely, therefore, they have claimed every article and blog on all websites. It also saves time on research and development while staying factual and accurate. They reflect a shift in Natural Language Processing (NLP) and are included in numerous applications, including writing help and customer service chatbots.

Advanced artificial intelligence has great risks that should be taken seriously. Consider an artificial intelligence designed to be merely destructive or, even worse, autonomous weapons-these results pose existential hazards. Giving an artificial intelligence human whimsy control over issues that might call for autonomous weaponry could inadvertently escalate a scenario to disastrous consequences.

Similarly, artificial intelligence can still be harmful; if it is goal-aligned, it can be devoted to good reasons, but you might still run a great risk. The scenario of self-driving automobiles illustrates how this might go wrong. In some situations, the raw, literal following of rules would perhaps predict wrong actions for carrying out their intended purpose, hence somewhat acting that might result in an undesirable or dangerous consequence to human life. Therefore, as artificial intelligence becomes autonomous, we surely have to control our systems to guarantee they make decisions grounded in human values.

Future impact of AI in different sectors

Healthcare

AI will play a vital role in the healthcare sector for diagnosing diseases quickly and more accurately. New drug discovery will be faster and cost-effective with the help of AI. It will also enhance the patient engagement in their care and also make ease appointment scheduling, bill paying, with fewer errors. However, apart from these beneficial uses, one great challenge of AI in healthcare is to ensure its adoption in daily clinical practices.

Cyber security

Undoubtedly, cyber security is a priority for each organization to ensure data security. There are some predictions that cyber security with AI will have below changes:

• With AI tools, security incidents will be monitored.
• Identification of the origin of cyber-attacks with NLP.
• Automation of rule-based tasks and processes with the help of RPA bots.

However, being a great technology, it can also be used as a threat by attackers. They can use AI in a non-ethical way by using automated attacks that may be intangible to defend against.

Transportation

The fully autonomous vehicle is not yet developed in the transportation sector, but researchers are making progress in this field. AI and machine learning are being applied in the cockpit to help reduce workload, handle pilot stress and fatigue, and improve on-time performance. There are several challenges to the adoption of AI in transportation, especially in areas of public transportation. There’s a great risk of over-dependence on automatic and autonomous systems.

E-commerce

Artificial Intelligence will play a vital role in the e-commerce sector shortly. It will positively impact each aspect of the e-commerce sector, ranging from user experience to marketing and distribution of products. We can expect e-commerce with automated warehouse and inventory, shopper personalization, and the use of chatbots in the future.

Employment

Nowadays, employment has become easy for job seekers and simple for employers due to the use of Artificial Intelligence. AI has already been used in the job search market with strict rules and algorithms that automatically reject an employee’s resume if it does not fulfil the requirement of the company. It is hoping that the employment process will be driven by most AI-enabled applications ranging from marking the written interviews to telephonic rounds in the future.

For jobseekers, various AI applications are helping build awesome resumes and find the best job as per your skills, such as Rezi, Jobseeker, etc.

Apart from the above sectors, AI has great future in manufacturing, finance & banking, entertainment, etc.

Finance

In several forms throughout the financial services sector, artificial intelligence is being applied. AI algorithms have a notable role in fraud detection; certain AI applications may find abnormal transaction patterns that could be fraud by analyzing transaction activity. AI systems, for instance, can rapidly analyze millions of market data items to assist in understanding quick trade execution needed to enhance returns, therefore significantly affecting algorithmic trading.

Using AI, robo-advisors generate customized investment recommendations dependent on profiles of risk tolerance, personal goals, and the investment horizon. Furthermore, consumer care contacts are starting to utilize AI powered software in the shape of chatbots, which can respond to inquiries, provide account and transactional activity, connect people to other financial resources, and guidance and advice.

Education

AI will progressively personalize and improve our educational experience. AI-powered learning systems will evaluate student performance and tailor the pedagogic curriculum to fit every person’s needs and learning preferences. While simulating virtual teaching assistants, intelligent tutoring systems will give students individualized comments and suggestions.

Artificial Intelligence (AI) has affected several industries by advancing their performance, decreasing the margin of errors, and improving decision-making. It saves time through outsourcing activities, handling big volumes of data, and enabling others, such as smart devices and self-driving cars. AI also has positive effects on the development of the healthcare, education and financial sectors.

However, it comes with challenges. There are two types of concerns related to AI; there could be unemployment because of dependency on such systems, and more to the point, algorithms are designed, and if these are flawed, prejudiced decisions could be made. Another risk involves privacy, and the possibility of using AI for negative intents is also another risk. Therefore, it is clear that the use of AI seems to be a boon that comes with certain consequences that may be deemed a curse.

Advantages of Artificial Intelligence (AI)

There are an enormous number of advantages to artificial intelligence. Some of them are as follows:

Reduction in Human Error

One of the biggest achievements of Artificial Intelligence is that it can reduce human error. Unlike humans, a computer machine can’t make mistakes if programmed correctly, while humans make mistakes from time to time. Therefore, Artificial Intelligence uses some set of algorithms by gathering previously stored data, reducing the chances of error and increasing the accuracy and precision of any task. Hence, artificial intelligence helps solve complex problems that require difficult calculations and can be done without any error.

Reduce the Risk (Zero Risk)

It is also one of the biggest advantages of Artificial Intelligence. The technology of developing AI Robots can overcome many risky limitations of humans and do dangerous things for us, such as defusing a bomb, oil and coal mining, exploring the deepest part of the ocean, etc. So, it helps in any worst situation, either human or natural disasters. AI Robots can be used in such situations where intervention can be hazardous.

24/7 Support

As humans need some breaks or refreshment after continuous working but a computer does not require breaks and refreshers. A normal human can continue to work for 8-9 hours, including breaks and refreshers, while a computer machine can work 24×7 without any breaks and don’t even get bored, unlike humans. Chatbots and helpline centers can be seen as the best examples of 24×7 support of various websites continuously engaged in receiving customers’ queries and automatically resolved by Artificial Intelligence.

Perform Repetitive Jobs

We perform so many repetitive works in our day-to-day life, such as automatic replies to emails, sending birthday and anniversary quotes and verifying documents, etc. Therefore, Artificial Intelligence (AI) helps to automate the business by performing these repetitive jobs.

Faster decision

Unlike humans, a machine helps to take decisions faster than a human and carry out actions quicker. While taking a decision, humans analyze many factors while the machine works on what it is programmed and delivers the results faster. The best example of the faster decision can be seen in an online chess game in the third level. It is impossible to beat a computer machine because it takes the best possible step in a very short time, according to the algorithms used behind it.

New Inventions

For new inventions, AI is helping humans almost in each sector, it can be healthcare, medical, educational, sports, technology, entertainment or research industry etc. Using advanced AI-based technologies, doctors can predict various dangerous diseases like cancer at a very early stage.

Daily Applications

Now, we are all completely dependent on mobile and the internet for our daily routine. We use several applications like Google Maps, Alexa, Apple’s Siri, Windows Cortana, and OK Google to take selfies, make phone calls, reply to mail, etc. Further, we can also predict the weather for today and upcoming days with the help of various AI-based methods.

Digital Assistance

Digital Assistance is one of the most powerful methods that help various highly advanced organizations interact with users without engaging human resources. Digital Assistance helps users by gathering previous users’ queries and providing solutions that users want. The best example of digital Assistance can be seen on various websites in the form of chatbot support.

A user asks something, and the computer machine provides relevant information like banking, education, travel, and ticket booking sites. Some chatbots are designed so that it’s become hard to determine whether we’re chatting with a chatbot or a human being.

AI in risky situations

Human safety is always the primary thing that is also taken care by machines. Whenever we need to explore the deepest part of the ocean or study space, scientists use AI-enabled machines in risky situations where human survival becomes difficult. AI can reach at every place where humans can’t reach.

If something has a bright side, then parallelly, it also has some dark side. Similarly, Artificial intelligence also has a few drawbacks that are as follows:

Disadvantages of Artificial Intelligence (AI)

Although artificial intelligence is one of the most trending and demanding technology around the globe, it still has some disadvantages. Some of the common disadvantages of AI are as follows:

High production cost

We are living in a technological world where we have to manipulate ourselves according to society. Similarly, a computer machine also requires time to time software and hardware updates to meet the latest requirements. Hence, AI also need repairing and maintenance, which need plenty of costs.

Risk of Unemployment

A robot is one of the implementations of Artificial intelligence, and it is replacing jobs and leading to serve unemployment (In some cases). Hence, according to some people, there is always a risk of unemployment because of robots and chatbots instead of humans. For example, in some more technology-oriented countries such as Japan, robots are widely used in manufacturing industries to replace human resources. However, this is not always the truth because as it replaces humans to enhance efficiency, it is also making more jobs opportunities for humans.

Increasing human’s laziness

As new inventions in the field of Artificial Intelligence are happening, it is making humans lazier towards their work, and the bad consequences of this advancement are that humans are becoming completely dependent on machines and robots. If these new inventions continue even for the next few years, then the next generations will become completely dependent on machines and robots, and the result will be vast unemployment and several health issues.

Emotionless

We have always learned since childhood that computers or machines don’t have emotions. Humans work like a team, and team management is a key factor for completing a target. However, there is no doubt that machines are much better when working efficiently, but it is also true that they never replace the human’s connection that makes the team.

Lack of creativity

The biggest disadvantage of Artificial Intelligence is its lack of creativity. Artificial Intelligence is a technology that is completely based on pre-loaded data. However, Artificial Intelligence can learn over time with this pre-fed data and past experiences, but it cannot be creative like humans.

No Ethics

Ethics and morality are the two most important features of humans, but it isn’t easy to incorporate both of these into Artificial Intelligence. AI is rapidly increasing uncontrollably in each sector, so if this continues for the upcoming decades, it may eventually wipe out humanity.

No improvement

Artificial Intelligence is a technology completely based on pre-loaded data and experience, so it cannot be improved as human. It can perform the same task repeatedly, but if you want some improvement and changes, you have to change the command for the same. However, it can store unlimited data that humans cannot, but also it cannot be accessed and used like human intelligence.

Conclusion

Artificial intelligence (AI) has numerous benefits, such as enhancing productivity, replacing certain human activities in various processes, improving decision-making capabilities, and enabling the analysis of large amounts of data. It improves sectors such as the health sector, the financial sector, and the transport sector, among others, as it accelerates the rate of invention and production. However, similar to any other technology in the world, AI also has returns that come with the added risks of more job losses, ethical issues, violation of privacy, and bias.

It is efficient and convenient to source all the analytical needs from AI, but it should not be included among the above options. Therefore, introducing AI into this field should be carried out gradually, assessing the benefits and actively having ethical and safe trials. Thus, society should be able to overcome those challenges that are provided by AI and, at the same time, promote those benefits that would be necessary to create the best world for everyone.

AI can be classified under different forms depending on the capabilities and the functions it possesses. These types are useful in comprehending the development and working of AI in various situations. It is possible to identify the simplest divisions between Narrow AI, General AI, and Super AI as the most basic ones, connecting the competence levels and the abilities to make decisions.

Another is based on the functioning of the AI: the reactive and limited memory machines, which possess the theory of mind and are self-conscious. With such a classification, one can think about the current position held by AI and predict the potential consequences it can bring to the community and technology.

AI Types

Artificial Intelligence is categorized into various means, which are basically classified into two broad criteria, i.e., capabilities and functionality.

AI Type 1: Based on Capabilities

1. Weak AI or Narrow AI: It is an AI that can be applied to particular problems and can adopt a specific type of work. When it is used in a certain region, it works, and when it is applied in other areas, it does not bring the same results. It is applied to intelligent products, which are referred to as virtual assistants like Siri, systems involved in image recognition and Watson of IBM.
2. General AI: General AI, which is alternatively referred to as Strong AI, is defined as machines that can perform any of the tasks that man can execute. It is expected to acquire human characteristics, including intelligence traits, e.g., learning as well as reasoning. This is another type of AI that is still under research and has not been developed to its realization.
3. Super AI: A powerful artificial intelligence where all fields perform higher than humans regarding their decision-making capabilities, problem-solving, learning abilities, emotions and feelings, etcetera. It is the last level of AI development, and it is not present in the world now.

AI Type 2: Based on Functionality

1. Reactive Machines: It is a kind of AI that acts on the present input data and lacks any prior experience. The best-known examples are the chess machine Deep Blue, developed by IBM, and the Go-play computer called Google AlphaGo.
2. Limited Memory: Most of them make use of the previous information to settle some short-run. Examples of some of the concrete samples are the self-driving cars that follow other vehicles and the speed and the quality of the road where these cars are driving.
3. Theory of Mind: This AI aims to understand the feelings, desires or even gestures of people. As it has been mentioned above, it remains a part of the theoretical studies and is not fully manifested.
4. Self-Awareness: The last form of artificial intelligence that would still be at the theoretical stage is more advanced than the intelligence of man as it would be conscious and emotional. People would also view such a level of AI as a considerable advancement not only on the technological level but also on the level of knowledge.

Conclusion

AI is found in various forms, and the differences put it in a better picture concerning development and applicability. Beginning with the minimum form of artificial intelligence within the apps and going all the way to the Super AI, each level leads to the growth of technological change. The functional types also show the way the systems perform on the data and the user.

Representatives of the research, development, and policymaker will find it necessary to get to know these categories in order to utilize AI smartly and effectively. That is why the specified categories can alter with technology evolving and develop new notions and anticipations regarding the work of intelligent systems in the future.

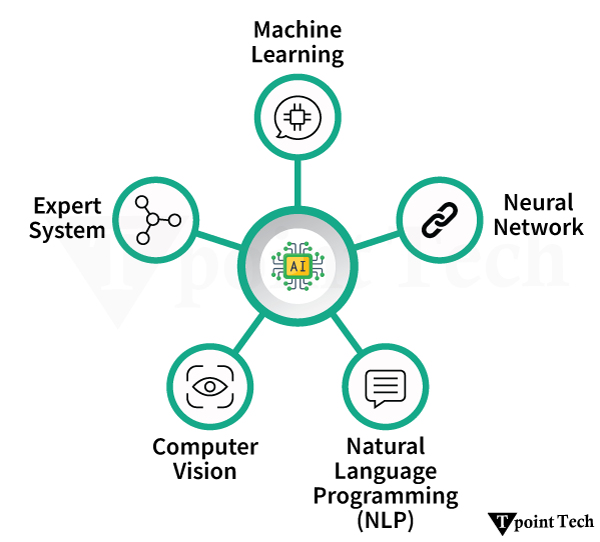
The term “Artificial Intelligence” refers to the simulation of human intelligence processes by machines, especially computer systems. It also includes Expert systems, voice recognition, machine vision, and natural language processing (NLP).

AI programming focuses on three cognitive aspects such as learning, reasoning, and self-correction.

• Learning Processes
• Reasoning Processes
• Self-correction Processes

Learning Processes

This part of AI programming is concerned with gathering data and creating rules for transforming it into useful information. The rules, which are also called algorithms, offer computing devices with step-by-step instructions for accomplishing a particular job.

Reasoning Processes

This part of AI programming is concerned with selecting the best algorithm to achieve the desired result.

Self-Correction Processes

This part of AI programming aims to fine-tune algorithms regularly in order to ensure that they offer the most reliable results possible.

Artificial Intelligence is an extensive field of computer science that focuses on developing intelligent machines capable of doing activities that would normally require human intelligence. While AI is a multidisciplinary science with numerous methodologies, advances in deep learning and machine learning create a paradigm shift in almost every aspect of technology.

Examples of AI

The following are examples of AI-Artificial Intelligence:

1. Google Maps and Ride-Hailing Applications
2. Face Detection and Recognition
3. Text Editors and Autocorrect
4. Chatbots
5. E-Payments
6. Search and Recommendation Algorithms
7. Digital Assistant
8. Social Media
9. Healthcare
10. Gaming
11. Online Ads-Network
12. Banking and Finance
13. Smart Home devices
14. Security and Surveillance
15. Smart Keyboard App
16. Smart Speaker
17. E-Commerce
18. Smart Email Apps
19. Music and Media Streaming Service
20. Space Exploration

Let’s discuss the above examples in detail.

1. Google Maps and Ride-Hailing Applications

Traveling to a new destination does not require much thought any longer. Rather than relying on confusing address directions, we can now easily open our phone’s map app and type in our destination.

So how does the app know about the appropriate directions, the best way, and even the presence of roadblocks and traffic jams? A few years ago, only GPS (satellite-based navigation) was used as a navigation guide. However, artificial intelligence (AI) now provides users with a much better experience in their unique surroundings.

The app algorithm uses machine learning to recall the building’s edges that are supplied into the system after the person has manually acknowledged them. This enables the map to provide simple visuals of buildings. Another feature is identifying and understanding handwritten house numbers, which assists travelers in finding the exact house they need. Their outline or handwritten label can also recognize locations that lack formal street signs.

The application has been trained to recognize and understand traffic. As a result, it suggests the best way to avoid traffic congestion and bottlenecks. The AI-based algorithm also informs users about the precise distance and time it will take them to arrive at their destination. It has been trained to calculate this based on traffic situations. Several ride-hailing applications have emerged as a result of the use of similar AI technology. So, whenever you need to book a cab via an app by putting your location on a map, this is how it works.

2. Face Detection and Recognition

Utilizing face ID to unlock our phones and using virtual filters on our faces while taking pictures are two uses of AI that are presently essential for our day-by-day lives.

Face recognition is used in the former, which means that every human face can be recognized. Face recognition is used in the above, which recognizes a particular face.

Intelligent machines often match-and some cases, even exceed human performance. Human babies begin to identify facial features such as eyes, lips, nose, and face shapes. A face, though, is more than just that. A number of characteristics distinguish human faces.

Smart machines are trained in order to recognize facial coordinates (x, y, w, and h, which form a square around the face as an area of interest), landmarks (nose, eyes, etc.), and alignment (geometric structures). This improves the human ability to identify faces by several factors. Face recognition is also used by government facilities or at the airport for monitoring and security.

3. Text Editors or Autocorrect

When typing a document, there are inbuilt or downloadable auto-correcting tools for editors of spelling errors, readability, mistakes, and plagiarism based on their difficulty level.

It should have taken a long time for us to master our language and become fluent in it. Artificially intelligent algorithms often use deep learning, machine learning, and natural language in order to detect inappropriate language use and recommend improvements. Linguists and computer scientists collaborate in teaching machines grammar in the same way that we learned it in school.

Machines are fed large volumes of high-quality data that have been structured in a way that machines can understand. Thus, when we misspell a single comma, the editor will highlight it in red and offer suggestions.

4. Chatbots

Answering a customer’s inquiries can take a long time. The use of algorithms to train machines to meet customer needs through chatbots is an artificially intelligent solution to this problem. This allows machines to answer as well as take and track orders.

We used Natural Language Processing (NLP) to train chatbots to impersonate customer service agents’ conversational approaches. Advanced chatbots do not require complex input formats (such as yes/o questions). They are capable of responding to complex questions that necessitate comprehensive answers.

They will appear to be a customer representative, in fact, another example of artificial intelligence (AI). If you give a negative rating to a response, the bot will figure out what went wrong and fix it the next time, ensuring that you get the best possible service.

5. Online-Payments

It can be a time-consuming errand to rush to the bank for any transaction. Good news! Artificial Intelligence is now being used by banks to support customers by simplifying the process of payment.

Artificial intelligence has enabled you to deposit checks from the convenience of your own home. Since AI is capable of deciphering handwriting and making online cheque processing practicable, artificial intelligence can potentially be utilized to detect fraud by observing consumers’ credit card spending patterns.

For example, the algorithms are aware of what items User X purchases, when and where they are purchased, and in what price range they are purchased. If there is some suspicious behavior that does not match the user’s profile, then the system immediately signals user X.

6. Search and Recommendation Algorithms

When we wish to listen to our favorite songs, watch our favorite movie, or shop online, have we ever found that the things recommended to us perfectly match our interests? This is the beauty of artificial intelligence.

These intelligent recommendation systems analyze our online activity and preferences to provide us with similar content. Continuous training allows us to have a customized experience. The data is obtained from the front end, saved as big data, and analyzed using machine learning and deep learning.

Then, it can predict your preferences and make suggestions to keep you amused without having to look for something else. Artificial intelligence can also be utilized to improve the user experience of a search engine. Generally, the answer we are searching for is found in the top search results. What causes this?

Data is fed into a quality control algorithm to identify high-quality content from SEO-spammed, low-quality content. This aids in creating an ascending order of search results on the basis of the quality for the greatest user experience. Since search engines are made up of codes, natural language processing technology aids in understanding humans through these applications; in reality, they can predict what a person wants to ask by compiling top-ranked searches and guessing their questions when they begin to type.

Machines are constantly being updated with new features such as image search and voice search. If we need to find out a song that is playing at a mall, all we have to do is hold the phone up to it, and a music-identifying app will tell us what it is within a few seconds. The machine will also offer you song details after searching through an extensive collection of tunes.

7. Digital Assistants

When our hands are full, we often enlist the help of digital assistants to complete tasks on our behalf. We might ask the assistant to call our father while we are driving with a cup of tea in one hand. For instance, Siri would look at our contacts, recognize the word “father,” and dial the number.

Siri is an example of a lower-tier model that can only respond to voice commands and cannot deliver complex responses. The new digital assistant is fluent in human language and uses advanced NLP (Natural Language Processing) and ML (Machine Learning) techniques. They are capable of understanding complex command inputs and providing acceptable results.

They have adaptive abilities that can examine preferences, habits, and schedules. It enables them to use prompts, schedules, and reminders to help us systemize, coordinate, and plan things.

8. Social Media

The advent of social media gave the world a new narrative with immense freedom of speech. Although, it brought certain social ills like cyberbullying, cybercrime, and abuse of language. Several social media apps are using AI to help solve these issues while also providing users with other enjoyable features.

AI algorithms are much quicker than humans at detecting and removing hate speech-containing messages. It is made possible by their ability to recognize hostile terms, keywords, and symbols in a variety of languages. These have been entered into the system, which can also contribute neologisms to its dictionary. Deep learning’s neural network architecture is a vital part of the process.

Emojis have become the most common way to express a wide range of emotions. This digital language is also understood by AI technology because it can understand the meaning of a certain piece of text and guess the exact emoji.

Social networking, a perfect example of artificial intelligence, may even figure out what kind of content a user likes and recommends similar content. Facial recognition is also used in social media profiles, assisting users in tagging their friends via automatic suggestions. Smart filters can recognize spam and undesirable messages and automatically filter them out. Users may also take advantage of smart answers.

The social media sector could use artificial intelligence to detect mental health issues such as suicidal thoughts by analyzing the information published and consumed. This information can be shared with mental health professionals.

9. Healthcare

Infervision is using artificial intelligence and deep learning to save lives. In China, where there are insufficient radiologists to keep up with the demand for checking 1.4 billion CT scans each year for early symptoms of lung cancer. Radiologists are essential to review many scans every day, which isn’t just dreary, yet human weariness can prompt errors. Infervision trained and instructed algorithms to expand the work of radiologists in order to permit them to diagnose cancer more proficiently and correctly.

The inspiration and foundation for Google’s DeepMind is Neuroscience, which aims to create a machine that can replicate the thinking processes in our own brains. While DeepMind has effectively beaten people at games, what is truly captivating are the opportunities for medical care applications. For example, lessening the time it takes to plan treatments and utilizing machines to help diagnose ailments.

10. Gaming

Artificial Intelligence has been an important part of the gaming industry in recent years. In reality, one of AI’s most significant achievements is in the gaming industry.

One of the most important achievements in the field of AI is DeepMind’s AI-based AlphaGo software, which is famous for defeating Lee Sedol, the world champion in the game of GO. Shortly after the win, DeepMind released AlphaGo, which trounced its predecessor in an AI-AI face-off. The advanced machine, AlphaGo Zero, taught itself to master the game, unlike the original AlphaGo, which DeepMind learned over time using a vast amount of data and supervision.

Unlike the first AlphaGo, which DeepMind prepared over the long run by utilizing a lot of information and oversight, the high-level framework AlphaGo Zero instructed itself to dominate the game. Another example of Artificial Intelligence in gaming comprises the First Encounter Assault Recon, also known as F.E.A.R, which is the first-person shooter video game.

11. Online Ads Network

The online advertising industry is the most significant user of artificial intelligence that uses AI (Artificial Intelligence) to not only monitor user statistics but also to advertise on the basis of statistics. The online advertising industry will struggle if AI is not implemented, as users will be shown random advertisements that have no relation to their interests.

Since AI has been so good at determining our preferences and serving us ads, the worldwide digital ad industry has crossed 250 billion US dollars, with the business projected to cross the 300 billion mark in 2019. So, the next time, remember that AI is changing your life while you browse the internet and encounter adverts or product recommendations.

12. Banking and Finance

The banking and finance industry has a major impact on our daily lives, which means the world runs on liquidity, and banks are the gatekeepers who control the flow. Did you know that artificial intelligence is heavily used in the banking and finance industry for things such as customer service, investment, fraud protection, and so on? The automatic emails we get from banks if we make an ordinary transaction are a simple example.

That’s AI keeping an eye on our account and trying to alert us regarding any potential fraud. AI is now being trained to examine vast samples of fraud data in order to identify patterns so that we can be alerted before it happens to us. If we run into a snag and contact our bank’s customer service, we are probably speaking with an AI bot. Even the largest financial industry uses AI to analyze data in order to find the best ways to invest capital in order to maximize returns while minimizing risk.

Not only that, but AI is set to play an even larger role in the industry, with major banks around the world investing billions of dollars in AI technology, and we will be able to see the results sooner rather than later.

13. Smart Home Devices

Another popular example of AI (Artificial Intelligence) is smart home devices. Artificial intelligence is even being welcomed into our homes. Most of the smart home gadgets we purchase use artificial intelligence to learn our habits and automatically change settings to make our experience as seamless as possible.

We have effectively examined how we utilize savvy voice assistants to control these smart home gadgets. We probably are aware that it is a great example of AI’s impact on our lives. That is to say, there are smart thermostats that change the temperature depending on our preferences, smart lights that change the color and intensity of lights depending on time, and much more. This will not happen when our primary interaction with all our smart home devices is only through AI.

14. Security and Surveillance

Although we all can debate about the ethics of using a large surveillance system, there’s no denying that it’s being used, and AI is playing a significant role in it. It isn’t workable for people to keep monitoring many monitors simultaneously, and thus, utilizing AI makes sense. With technologies such as facial recognition and object recognition improving every day, it won’t be long before all the security cameras dealt with are checked by an AI and not a human. Right now, before AI can be completely implemented, this is going to be our future.

15. Smart Keyboard Apps

Smart keyboard apps are another example of AI (Artificial Intelligence). In all actuality, not every person loves managing on-screen keyboards. Although, they have become far more intuitive, permitting clients to type comfortably and quickly. What has likely ended up being a catalyst for them is the integration of AI. The smart keyboard applications keep a tab on the composing style of a client and predict words and emojis based on that. Consequently, typing on the touchscreen has gotten quicker and more advantageous. Not to mention that artificial intelligence is crucial in detecting misspellings and typos.

16. Smart Speakers

Not in vain; many think that smart speakers are good to go for a major blast into technology. Besides controlling smart home gadgets, they are likewise capable of various things like sending fast messages, setting updates, checking the climate, and getting the most recent news.

Also, it’s this flexibility that ends up being a conclusive factor for them. Driven by the hugely popular Amazon Echo series, the worldwide brilliant speaker market arrived at an exceptional high in 2019 with sales of 149.9 million units, which is a huge increment of 70% in 2018. Additionally, the sales in Q4 2019 also saw another record with an incredible 55.7 million units. Smart speakers are likely the most unmistakable instances of the utilization of AI in our reality.

17. E-Commerce

Artificial intelligence algorithms have given the necessary vital impulse to web-based businesses to give a more customized insight. According to many sources, its use has significantly improved sales and has also aided in developing long-term consumer relationships. Thus, organizations take advantage of AI to deploy chatbots to gather urgent information and predict purchases to make a client-centric experience.

On the way across this shift of technique? Simply invest some time on websites such as Amazon and eBay, and we will soon see how quickly the scene around you is improving rapidly!

18. Smart Email Apps

In the event that you actually find your inbox cluttered with an excessive number of undesirable messages, the possibility is quite high that we can yet stay with an old-fashioned email application.

Present-day email applications such as Spark make several AI to filter out spam messages and furthermore arrange messages so you can rapidly get to the significant ones. Likewise, it additionally provides smart answers dependent on the messages we get to help us answer any email rapidly. The “Smart Reply” highlight of Gmail is an extraordinary illustration of this. It utilizes AI to filter the content of the email and gives you context-oriented answers.

19. Music and Media Streaming Service

Another amazing illustration of how AI affects our lives is the music and media streaming features that we utilize reliably. Whether or not you are utilizing Spotify, Netflix, or YouTube, AI is making the decisions for you.

All things considered, everything, once in a while, is great, and some of the time is awful. For instance, I enjoy Spotify’s Discover Weekly playlist since it has acquainted me with a few new artists who I would not have known about if it weren’t for Spotify’s AI divine beings.

Then again, I additionally remember going down the YouTube rabbit hole, wasting uncountable hours simply watching the suggested videos. That suggested videos section has become so great at knowing my taste that it’s alarming. Thus, keep in mind that AI is at work whenever you are watching a suggested video on YouTube, viewing a suggested show on Netflix, listening to a pre-made playlist on Spotify, or using any other media and music streaming service.

20. Space Exploration

Space expeditions and discoveries consistently require investigating immense measures of information. Artificial Intelligence and Machine learning are the best approaches for dealing with and measuring information on this scale. After thorough astronomers and research utilized Artificial Intelligence to filter through long periods of information obtained by the Kepler telescope to distinguish an inaccessible eight-planet solar system.’

21. Cybersecurity

AI plays a very key role in transforming roles in modern cybersecurity. It helps in detecting the threat more consistently while being fast and more accurate. It also works as a response system that takes care of the attacks that happened and retaliates them.

AI does all these through machine learning and deep learning techniques that only learn from all the previous data and try to find the patterns that might help in identifying the malicious activity. For context, it can detect unauthorized data access and underlying anomalies in the network that might help track a cyber attack.

AI-powered solutions that imitate the human immune system are used by businesses such as Darktrace to automatically identify and eliminate threats in real time. In a similar vein, Microsoft’s Azure Sentinel and IBM’s QRadar use AI to evaluate enormous volumes of log data and identify security events with high precision, lowering the number of false positives.

22. Agriculture

Smart agriculture takes the help of AI to change conventional farming methods, and that makes it more cost-efficient and sustainable. Drones, Heat-sensor and CVs are used as a form or medium to collect data on the farming aspects. This data enables farmers to make informed decisions that can greatly increase crop yields and resource management. AI systems, for instance, are able to identify early indicators of illness or nutritional deficiencies in crops, enabling prompt treatments to stop losses.

The See & Spray platform from John Deere, which uses cutting-edge computer vision to differentiate between crops and weeds, is a useful example of this technology in action. It makes it possible to apply herbicides precisely where they are needed, which minimizes the impact on the environment, lowers expenses, and uses fewer chemicals. AI is assisting in the transformation of agriculture into a data-driven, sustainable sector that can satisfy the rising need for food on a worldwide scale with such advancements.

23. Weather Forecast

Based on current data and worldwide trends, artificial intelligence algorithms can assist numerous weather forecasting applications in making quick predictions about the weather. Compared to conventional techniques, these models save money and energy and can offer continuous updates and information changes.

In a number of tests, they have outperformed humans in accuracy, and their use is growing. GraphCast, a machine learning and artificial intelligence model financed by Alphabet and Google DeepMind, is a recent example of this. This model surpasses current industry standards on 90% of evaluated variables and can forecast hundreds of weather variables globally.

24. Autonomous Vehicle

Autonomous Vehicles, or self-driving cars, are a revolutionary use of AI in the field of transportation. Using a combination of AI algorithms, sensors, cameras, radar, and LIDAR, these cars analyze their environment, make driving decisions, and operate without human input. Just as a human driver would analyze data from their eyes and ears, AI uses data from the sensors in real-time to detect hazards in the environment, identify traffic signals, follow lanes, and adapt to changing road conditions, including other traffic and weather.

For example, autonomous vehicles can anticipate the behavior of pedestrians and other vehicles in order to make appropriate decisions for safe and efficient driving. A familiar real-world application is Tesla’s Autopilot system. Tesla has developed an AI-powered system that uses standard cruise control but also offers features like automatic lane-keeping, adaptive cruise control, and self-parking.

25. Evaluating Learning and Student Feedback

The education sector is being positively transformed, specifically regarding assessment, with greater efficiency and insight made possible through artificial intelligence (AI). The application of an AI algorithm can autonomously evaluate assessments, which minimizes grading time for teachers while keeping evaluation consistent.

In addition to scoring students’ assessments, AI can identify patterns in student responses to determine common areas of struggle. For example, if a [concerning] number of students get a question wrong, AI will notify the instructor to suggest that the related content may need to be retaught or clarified. The benefits of assessments, when combined with feedback based on data, strengthen a teacher’s ability to improve learning and address gaps.