Author: saqibkhan

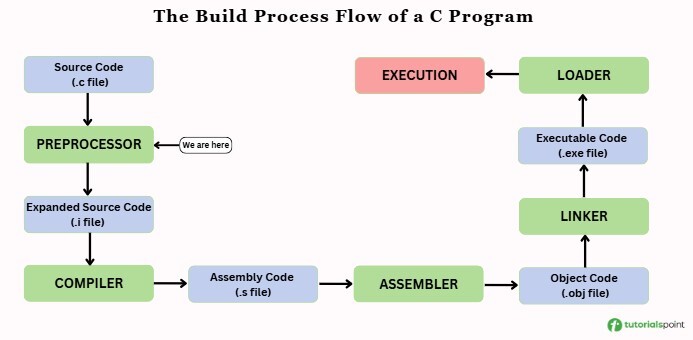
When we write a C program, it goes through multiple steps before becoming an executable file. The very first step is preprocessing, which is handled by the C Preprocessor. It prepares the source code for compilation by processing all instructions that start with the # symbol, called preprocessor directives.

Here is the overall build process of a C program, showing where the preprocessor comes in −

In this chapter, we’ll see what the preprocessor does, how it works, and why it is important in a C program.

What is a preprocessor?

The preprocessor is a program that executes at the very first stage of compilation. It looks for preprocessor directives and performs tasks like including header files, defining constants, or selectively compiling parts of the code. It returns the modified source code with the ‘.i’ extension, which then goes to the assembler.

For example −

#include <stdio.h>#define PI 3.14

Here, #include and #define are preprocessor directives. #include uses standard functions, and #define creates a constant value for the program.

Main Functions of Preprocessor

The preprocessor works purely with text and does not understand C language syntax, variables, functions, or data types. It performs text manipulation based on preprocessor directives. Its main functions are −

• It removes all comments (// or /* */).
• It expands macros wherever they are used by replacing them with their definitions.
• It includes files based on standard header files or custom files.
• It selects only the required parts of the code for compilation.
• It adjusts line numbers, handles control and special instructions, throws errors, or gives special compiler instructions.

Working of Preprocessor in C

Let’s see the steps below to understand how internally our preprocessor works before the compilation process.

Step 1: Reading the File

The preprocessor opens your .c source file and reads it as plain text. It breaks the program into tokens, which are the smallest units like keywords, symbols, and numbers.

For example −

intmain(){return0;}

The tokens for this program will be: int, main, (, ), {, return, 0, ;, }. These tokens are used in the next steps to identify preprocessor instructions.

Step 2: Looking for Preprocessor Instructions

The preprocessor scans the program line by line to identify preprocessor directives. These lines always start with #, such as #include, #define, and #ifdef. At this step, it only marks these lines for further processing and does not act on them yet.

For example −

#include <stdio.h>   // Preprocessor instruction#define MAX 100      // Preprocessor instructionint x = MAX;// Normal C code

Here, only the lines starting with # are recognized as preprocessor instructions. The rest of the code is ignored at this step.

Step 3: Removing Comments

Before processing any directives, the preprocessor removes all comments from the code. This includes both single-line (//) and multi-line (/* */) comments.

For example –

// This is a single line commentint a =10;/* This is a block comment */

After preprocessing, it becomes –

int a =10;

Step 4: File Inclusion

Now the preprocessor processes the #include directives that were identified earlier. It opens the specified file and copies its entire content into the program.

For example, consider a main.c program and a myheader.h header file –

main.c

#include "myheader.h"intmain(){return0;}

myheader.h

#define PI 3.14intcalculate();

After preprocessing, it will look like this −

#define PI 3.14intcalculate();intmain(){return0;}

The #include line is replaced by the actual content of the header file.

Step 5: Macro Definition and Expansion

Macros are text replacements defined by the preprocessor. They can be object-like or function-like, and they are replaced wherever they appear in the code. Let’s see an example below −

Object-like Macros

#define MAX 100#define MIN 1int array[MAX];int value = MIN +5;

After preprocessing, the code becomes −

int array[100];int value =1+5;

Here, the preprocessor repalces MAX with 100 and MIN with 1.

Function like Macros

#define SQUARE(x) ((x) * (x))double result =SQUARE(5);

After preprocessing, it becomes −

double result =((5)*(5));

The processor works like a small inline function and repalces the function-like macro call with the actual expression. Here, SQUARE(5) is replaced with ((5) * (5)).

Step 6: Conditional Compilation

The preprocessor can also include or skip certain parts of the program depending on the conditions provided using directives like #if, #ifdef, and #ifndef.

For example −

#define DEBUG#ifdef DEBUGprintf("Debug mode\n");#elseprintf("Release mode\n");#endif

If DEBUG is defined, the program will print Debug mode and if it is not defined, the program will print Release mode.

Step 7: Line Control and Special Directives

The preprocessor also handles special directives that control the compiler or show custom messages. For example, #line can set custom line numbers in error messages, #error stops compilation and displays a message, and #pragma sends instructions to the compiler. These directives gives us more control over compilation and error reporting.

For example −

#error This program requires C99

Here, #error stops the compilation and shows a message that displays the program requires the C99 standard.

Step 8: Producing Modified Source Code

After processing all directives, expanding macros, including files, handling conditional compilation, and removing comments, the preprocessor generates the modified source code. This code is what the compiler actually works with.

For example, if main.c contains −

#include <stdio.h>#define MAX 5intmain(){int arr[MAX];printf("Array size is %d\n", MAX);return0;}

It will produce the main.i file. Normally, we don’t see the preprocessed file, but we can generate it using GCC like this −

gcc -E main.c -o main.i

Here, the -E option stops compilation after preprocessing and creates the main.i file −

#include <stdio.h>intmain(){int arr[5];printf("Array size is %d\n",5);return0;}

In this file, the macro MAX is replaced with 5, the content of <stdio.h> is included, and comments are removed.

Final Example: Working of Preprocessor

Let’s take a complete program example that uses different preprocessor directives and see how the preprocessor transforms the code for the next step of compilation process.

Original Code (main.c) −

#include <stdio.h>#define PI 3.14#define AREA(r) (PI * (r) * (r))#define DEBUGintmain(){#ifdef DEBUGprintf("Debugging Mode\n");#endifdouble result =AREA(5);printf("Area = %f\n", result);return0;}

Preprocessed Code (main.i) −

#include <stdio.h>intmain(){printf("Debugging Mode\n");double result =(3.14*(5)*(5));printf("Area = %f\n", result);return0;}

In the above program the preprocessor performs the following task before generating the file with .i extension.

• It replaced the macro PI with 3.14.
• It expanded the macro AREA(5) into (3.14 * (5) * (5)).
• It included the printf(“Debugging Mode\n“); line because DEBUG was defined.
• It processed the #include <stdio.h> directive by inserting the contents of the standard I/O header file.

In this chapter, we learned about the preprocessor, which is the first stage of the build process and prepares the source code for compilation. It takes the source file, processes all directives, macros, and comments, and generates an assembly file that is then passed to the assembler and linker, continuing through the build process to produce the final executable.

Macros in C are the names given to specific constant values or code statements which are replaced with their value/code before the compilation processor. C Macros are defined using the #define preprocessor directive.

Macros are useful for code reusability, defining constant values, defining inline functions, and conditional compilations.

The following are the different types of C macros that we are going to cover in this tutorial –

• Object-like Macros
• Function-like Macros
• Chained Macros
• Variadic Macros
• Predefined Macros

Object-like Macros

A macro that defines a constant is an object-like macro.

Syntax

It is done with the following syntax −

#define name value

Example of Object-like Macros

In the following example, we are defining an object-like macro −

#include <stdio.h>// Defining macros#define PI 3.14#define MAX 10intmain(){// Printing the valuesprintf("Value of PI = %d\n", PI);printf("Value of MAX = %d\n", MAX);return0;}

Function-like Macro

To define a function-like macro, you use the same “#define” directive, but you put a pair of parentheses immediately after the macro name, with one or more arguments. Such a macro is expanded only when its name appears with a pair of parentheses after it.

When the preprocessor expands such a macro, it incorporates the specified arguments in the replacement text. The function-like macros are often called Macros with parameters (or arguments).

Syntax

A function-like macro is defined as follows −

#define macro_name([parameter_list]) replacement_text

Example of Function-like Macros

An example of function-like macro is given below −

#include <stdio.h>#define square(x) ((x) * (x))intmain(){int x =5;printf("x: %d \tSquare of x: %d", x,square(x));return0;}

Output

When you run this code, it will produce the following output −

x: 5 	Square of x: 25

Rules for Defining Function-like Macros

Some rules of defining a function also apply to macros −

• A macro can be defined without arguments
• A macro can be defined with a fixed number of arguments
• A macro can be defined with a variable number of arguments

For example, when you use such a macro, the comma-separated argument list must contain as many arguments as there are parameters in the macro definition.

Function-like Macros without Arguments

A function-like macro may also be defined without arguments.

Example 1

The following example shows how you can use a macro without arguments −

#include <stdio.h>#define MESSAGE() printf("Hello World");intmain(){int x =5;MESSAGE();return0;}

Output

Run the code and check its output −

Hello World

Some standard libraries also provide macro definitions in it. For example, the getchar() macro when expanded, implements the getc() function as follows −

#define getchar() getc(stdin)

Similarly, the putchar() macro encapsulates the putc() function −

#define putchar(x) putc(x, stdout)

Example 2

The following program defines a macro named as LOOP(x) and runs a for loop for the number of times as its argument −

#include <stdio.h>#define LOOP(x) {\
   for (int i = 1; i <= x; i++)\
   printf("Iteration no: %d\n", i);\
}intmain(){int x =3;LOOP(x);}

Output

When you run this code, it will produce the following output −

Iteration no: 1
Iteration no: 2
Iteration no: 3

Chained Macros

When we have a macro nested inside another macro, they are called Chained Macros.

Example of Chained Macros

The following example shows how you can use chained macros −

#include <stdio.h>#define PI 3.142#define CIRCUMFERENCE(x) (2*PI*x)intmain(){int x =5;printf("Circumference of a circle with radius %d is %f", x,CIRCUMFERENCE(x));return0;}

Output

When you run this code, it will produce the following output −

Circumference of a circle with radius 5 is 31.420000

Variadic Macros

You can also define a macro with variable number of arguments or variadic macros. A macro with variable-length argument is a feature that enables a macro to accept any number of arguments. You can pass positional as well as keyword arguments to a macro.

When a variadic macro is defined, the ellipsis () is given as an argument to capture variable number of arguments. To use variadic macros, the ellipsis may be specified as the final formal argument in a macro definition. This sequence of tokens replaces the identifier __VA_ARGS__ in the macro body wherever it appears.

The __VA_ARGS__ is replaced by all of the arguments that match the ellipsis, including commas between them. Note that the variadic macros can be used only in the C99 compatible C compilers and above.

Example of Variadic Macros

Take a look at the following example −

#include <stdio.h>#define MAX_ARGS 5		// Define maximum number of allowed arguments#define ARGS(x, ...) do {\
   printf("%d\n", ##__VA_ARGS__); \
} while (0)intmain(){ARGS(1,2,3);// 3 argumentsARGS(1,2,3,4,5,6);// 6 arguments return0;}

Output

Run the code and check its output −

2
2

Predefined Macros

ANSI C defines a number of macros. Although each one is available for use in programming, the predefined macros should not be directly modified.

Macro	Description
__DATE__	The current date as a character literal in “MMM DD YYYY” format.
__TIME__	The current time as a character literal in “HH:MM:SS” format.
__FILE__	This contains the current filename as a string literal.
__LINE__	This contains the current line number as a decimal constant.
__STDC__	Defined as 1 when the compiler complies with the ANSI standard.

Example

The following example demonstrates how you can use the predefined macros in a C program −

#include <stdio.h>intmain(){printf("File :%s\n",__FILE__);printf("Date :%s\n",__DATE__);printf("Time :%s\n",__TIME__);printf("Line :%d\n",__LINE__);printf("ANSI :%d\n", __STDC__ );}

Output

When you run this code, it will produce the following output −

File: main.c
Date: Mar 6 2024
Time: 20:12:19
Line: 8
ANSI: 1

What is #pragma Directive in C?

The preprocessor directive #pragma is used to provide additional information to the compiler in C/C++ language. This is used by the compiler to provide some special features.

Note that pragmas are compiler dependent. Not all the pragma directives are supported by all the compilers.

Syntax

Here is the syntax of using a #pragma directive in C/C++ language −

#pragma token_name

Types of Pragma Directives in C

The table of some of #pragma directives in C/C++ language is given as follows,

Directive	Description
#pragma startup	Before the execution of main(), the function specified in pragma is needed to run.
#pragma exit	Before the end of program, the function specified in pragma is needed to run.
#pragma warn	Used to hide the warning messages.
#pragma GCC dependency	Checks the dates of current and other file. If other file is recent, it shows a warning message.
#pragma GCC system_header	It treats the code of current file as if it came from system header.
#pragma GCC poison	Used to block an identifier from the program.
#pragma once	Compiler loads the header file only once.

#pragma startup and exit

These pragma directives are executed before and after the main() function. Not all the compilers support these directives.

Example

The following code demonstrates how you can use the pragma startup and exit directives −

#include <stdio.h>intdisplay();#pragma startup display#pragma exit displayintmain(){printf("\nI am in main function");return0;}intdisplay(){printf("\nI am in display function");return0;}

Output

When you run this code, it will produce the following output −

I am in main function

#pragma warn

The #pragma warn directive is used to hide or display the warning messages which are displayed during compilation.

The warn pragma is used as per the following syntax −

#pragma warn +xxx (To show the warning) #pragma warn -xxx (To hide the warning) #pragma warn .xxx (To toggle between hide and show)

The three character codes to be used are rvl (return value), par (parameter used or not), and rch (if the code is unreachable).

If any character code is prefixed by “+”, it indicates to show the warning; prefixed by “” means indication to the compiler to hide warnings, and prefix by dot (.) is an instruction to the compiler to toggle between hide and display warnings.

Example

The following example shows how you can use the warn pragma in a C program −

#include <stdio.h>#pragma warn -rvl          /* return value */#pragma warn +par	   /* parameter never used */#pragma warn rch	   /* unreachable code */intsquare(int x){printf("Hello World");}intmain(){square(10);return0;}

Output

When you run this code, it will produce the following output −

Hello World

#pragma GCC poison

The GCC compiler removes an identifier completely from the program. If we want to block an identifier, then we can use the #pragma GCC poison directive. Its syntax is as follows −

#pragma GCC poison identifier

Example

In this example, we will use the GCC poison pragma to block the printf() function −

#include <stdio.h>#pragma GCC poison printfintmain(){int a =10;if(a ==10){printf("Hello World");}elseprintf("TutorialsPoint");return0;}

Output

When you try to compile this code, it will show the following error −

error: attempt to use poisoned "printf"

#pragma GCC dependency

This pragma allows you to check the relative dates of the current file and another file. If the other file is more recent than the current file, a warning is issued.

Example

Take a look at the following example −

#include <stdio.h>#pragma GCC dependency "depends.c"intmain(){printf("Hello, World!");return0;}

Output

The above source code is depending on depends.c. If its compilation timestamp is more recent, then the following warning is issued −

warning: current file is older than depends.c

#pragma GCC system_header

As a convention, system header files are placed angular brackets in front of the #include directive, whereas the non-system header files are in quotation marks. If you want the compiler to treat the latter as the system header, use this pragma.

Syntax

#pragma GCC system_header

library.h

We define a “library.h” header file in the current directory.

#ifndef LIBRARY_H#define LIBRARY_H#pragma GCC system_headervoidmyFunction();#endif

Example

To ask the compiler to treat “library.h” as a system header, use the #pragma GCC system_header.

#include <stdio.h>#include "library.h"intmain(){myFunction();// Using a function from the library.hprintf("Hello, World!\n");return0;}

#pragma once

The #pragma once directive causes the header file to be included only once, even if the programmer includes it multiple times.

Save the “myheader.h” file as −

myheader.h

#pragma oncevoidmyFunction();

Example

In another code (main.c), call myFunction() as follows −

#include <stdio.h>#include "myheader.h"intmain(){myFunction();printf("Hello, World!\n");return0;}

Print Page

The C Preprocessor is not a part of the compiler, but is a separate step in the compilation process. In simple terms, a C Preprocessor is just a text substitution tool and it instructs the compiler to do the required pre-processing before the actual compilation. We’ll refer to the C Preprocessor as CPP.

In C programming, preprocessing is the first step in the compilation of a C code. It occurs before the tokenization step. One of the important functions of a preprocessor is to include the header files that contain the library functions used in the program. The preprocessor in C also defines the constants and expands the macros.

The preprocessor statements in C are called directives. A preprocessor section of the program always appears at the top of the C code. Each preprocessor statement starts with the hash (#) symbol.

Preprocessor Directives in C

The following table lists down all the important preprocessor directives −

Directive	Description
# define	Substitutes a preprocessor macro.
#include	Inserts a particular header from another file.
#undef	Undefines a preprocessor macro.
#ifdef	Returns true if this macro is defined.
#ifndef	Returns true if this macro is not defined.
#if	Tests if a compile time condition is true.
#else	The alternative for #if.
#elif	#else and #if in one statement.
#endif	Ends preprocessor conditional.
#error	Prints error message on stderr.
#pragma	Issues special commands to the compiler, using a standardized method.

Preprocessors Examples

Analyze the following examples to understand various directives.

This #define directive tells the CPP to replace the instances of MAX_ARRAY_LENGTH with 20. Use #define for constants to increase readability.

#define MAX_ARRAY_LENGTH 20

The following directives tell the CPP to get “stdio.h” from the System Libraries and add the text to the current source file. The next line tells CPP to get “myheader.h” from the local directory and add the content to the current source file.

#include <stdio.h>#include "myheader.h"

Now, take a look at the following #define and #undef directives. They tell the CPP to undefine existing FILE_SIZE and define it as 42.

#undef  FILE_SIZE#define FILE_SIZE 42

The following directive tells the CPP to define MESSAGE only if MESSAGE isn’t already defined.

#ifndef MESSAGE#define MESSAGE "You wish!"#endif

The following directive tells the CPP to process the statements enclosed if DEBUG is defined.

#ifdef DEBUG/* Your debugging statements here */#endif

This is useful if you pass the -DDEBUG flag to the gcc compiler at the time of compilation. This will define DEBUG, so you can turn debugging ON and OFF on the fly during compilation.

Predefined Macros in C

ANSI C defines a number of macros. Although each one is available for use in programming, the predefined macros should not be directly modified.

Macro	Description
__DATE__	The current date as a character literal in “MMM DD YYYY” format.
__TIME__	The current time as a character literal in “HH:MM:SS” format.
__FILE__	This contains the current filename as a string literal.
__LINE__	This contains the current line number as a decimal constant.
__STDC__	Defined as 1 when the compiler complies with the ANSI standard.

Example

Let’s try the following example −

#include <stdio.h>intmain(){printf("File: %s\n",__FILE__);printf("Date: %s\n",__DATE__);printf("Time: %s\n",__TIME__);printf("Line: %d\n",__LINE__);printf("ANSI: %d\n", __STDC__ );}

Output

When you run this code, it will produce the following output −

File: main.c
Date: Mar 6 2024
Time: 13:32:30
Line: 8
ANSI: 1

Preprocessor Operators

The C preprocessor offers the following operators to help create macros −

Example: The Macro Continuation (\) Operator in C

A macro is normally confined to a single line. The macro continuation operator (\) is used to continue a macro that is too long for a single line. Take a look at the following example −

#include <stdio.h>#define message_for(a, b)  \
   printf(#a " and " #b ": We love you!\n")intmain(){message_for(Ram, Raju);}

Output

When you run this code, it will produce the following output −

Ram and Raju: We love you!

Example: The Stringize (#) Operator in C

The stringize operator (#), also called number-sign operator, when used within a macro definition, converts a macro parameter into a string constant.

The stringize operator may be used only in a macro having a specified argument or parameter list. For example −

#include <stdio.h>#define  message_for(a, b)  \
   printf(#a " and " #b ": We love you!\n")intmain(){message_for(Carole, Debra);return0;}

Output

Run the code and check its output −

Carole and Debra: We love you!

Example: The Token Pasting (##) Operator in C

The token-pasting operator (##) within a macro definition combines two arguments. It permits two separate tokens in the macro definition to be joined into a single token. For example −

#include <stdio.h>#define tokenpaster(n) printf ("token" #n " = %d", token##n)intmain(){int token34 =40;tokenpaster(34);return0;}

Output

When you run this code, it will produce the following output −

token34 = 40

Example: The defined() Operator in C

The preprocessor defined operator is used in constant expressions to determine if an identifier is defined using #define. If the specified identifier is defined, the value is true (non-zero). If the symbol is not defined, the value is false (zero).

The following example shows how you can use the defined operator in a C program −

#include <stdio.h>#if !defined (MESSAGE)#define MESSAGE "You wish!"#endifintmain(){printf("Here is the message: %s\n", MESSAGE);return0;}

Output

Run the code and check its output −

Here is the message: You wish!

Parameterized Macros in C

One of the powerful functions of the CPP is the ability to simulate functions using parameterized macros. For example, we might have some code to square a number as follows −

intsquare(int x){return x * x;}

We can rewrite above the code using a macro as follows −

#define square(x) ((x) * (x))

Macros with arguments must be defined using the #define directive before they can be used. The argument list is enclosed in parentheses and must immediately follow the macro name. Spaces are not allowed between the macro name and open parenthesis.

Example

The following example demonstrates how you can use parameterized macros in C −

#include <stdio.h>#define MAX(x,y) ((x) > (y) ? (x) : (y))intmain(){printf("Max between 20 and 10 is %d\n",MAX(10,20));return0;}

Output

When you run this code, it will produce the following output −

Max between 20 and 10 is 20